Question

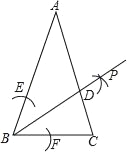
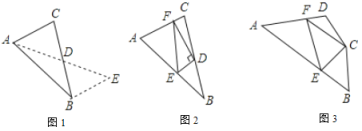
【题目】如图，在某次斯诺克比赛中，白球位于点 A 处，在点 A 正北方向的点 B 处有一颗红球，在点 A 正东方向 C 处有一颗黑球，在 BC 正中间的点 D 处有一颗篮球，其中点 C 在点 B 的南偏东 37°方向上，选手将白球沿正北方想推进 10cm 到达点 E 处时，测得点D 在点E 的北偏东45°方向上，求此时白球与红球的距离有多远？（参考数据：sin37°≈，cos37°≈ ，tan37°≈）

Answer 1

【答案】此时白球与红球的距离有 70cm 远．

【解析】

首先分析图形：根据题意构造直角三角形；本题涉多个直角三角形，应利用其公共边构造关系式，进而可求出答案．

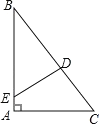
由题意可知，∠B=37°，∠DEB=45°，

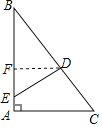
如图，过点D作DF⊥AC于点F，则DF∥AC，
设DF=xcm，
在Rt△BDF中，tan37°= ，即，则BF=cm，
在Rt△DEF中，tan45°=，即1=，
∴EF=xcm，
∵点D是BC中点，且DF∥AC，
∴BF=AF，
即=x+10，
解得x=30，
∴BE=70cm．
故此时白球与红球的距离有70cm远．