题目内容
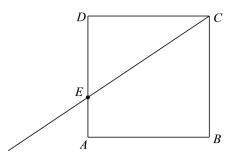
【题目】已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D点停止运动.作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF
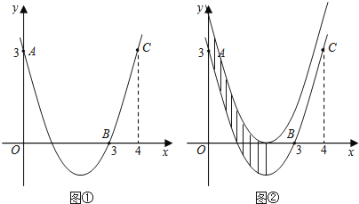
(1)依题意补全图形;
(2)猜想线段DE,EF,BF的数量关系并证明;
(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G运动的路线长.
【答案】(1)见解析;(2)EF=DE+BF,见解析;(3)2π
【解析】
(1)依题意补全图形即可;
(2)延长AD到点H,使DH=BF,连接CH,证明△CDH≌△CBF(SAS).得出CH=CF,∠DCH=∠BCF.证明△ECH≌△ECF(SAS).得出EH=EF.即可得出结论;
(3)确定点G的运动轨迹,利用弧长公式计算即可.
解:(1)补全图形如图1.
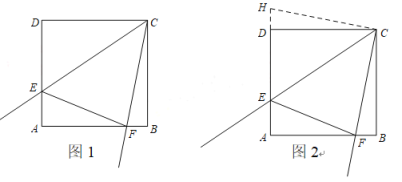
(2)线段DE,EF,BF的数量关系是 EF=DE+BF
证明:延长AD到点H,使DH=BF,连接CH(如图2).
易证△CDH≌△CBF.
∴CH= CF,∠DCH=∠BCF.
∵∠ECF=45°,
∴∠ECH=∠ECD+∠DCH= ∠ECD +∠BCF =45°.
∴∠ECH=∠ECF=45°.
又∵CE= CE,
∴△ECH≌△ECF.
∴EH= EF.
∴EF=DE+BF.
(3)点G运动的路线长为2π

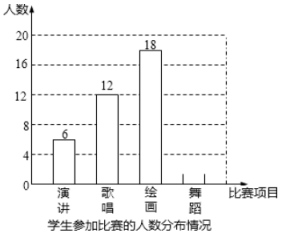
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由