题目内容
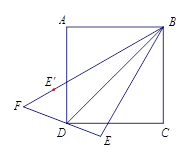
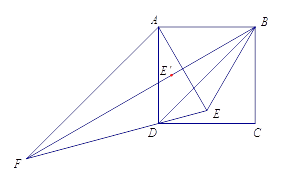
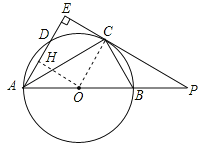
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
【答案】(1)证明见试题解析;(2)AB=3PB,理由见试题解析;(3)5.
【解析】
试题分析:(1)首先连接OC,由PE是⊙O的切线,AE和过点C的切线互相垂直,可证得OC∥AE,又由OA=OC,易证得∠DAC=∠OAC,即可得AC平分∠BAD;
(2)由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;
(3)首先过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,即可得AE=
,四边形OCEH是矩形,即可得AE=![]() +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
+OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
试题解析:(1)连接OC,∵PE是⊙O的切线,∴OC⊥PE,∵AE⊥PE,∴OC∥AE,∴∠DAC=∠OCA,∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OAC,∴AC平分∠BAD;
(2)线段PB,AB之间的数量关系为:AB=3PB.理由:
∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,∵OB=OC,∴∠OCB=∠ABC,∵∠PCB+∠OCB=90°,∴∠PCB=∠PAC,∵∠P是公共角,∴△PCB∽△PAC,∴![]() ,∴
,∴![]() =PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
=PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
(3)过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,∴OC=HE,∴AE=
,四边形OCEH是矩形,∴OC=HE,∴AE=![]() +OC,∵OC∥AE,∴△PCO∽△PEA,∴
+OC,∵OC∥AE,∴△PCO∽△PEA,∴![]() ,∵AB=3PB,AB=2OB,∴OB=
,∵AB=3PB,AB=2OB,∴OB=![]() PB,∴
PB,∴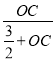 =
=![]() =
=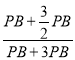 ,∴OC=
,∴OC=![]() ,∴AB=5,∵△PBC∽△PCA,∴
,∴AB=5,∵△PBC∽△PCA,∴![]() ,∴AC=2BC,在Rt△ABC中,
,∴AC=2BC,在Rt△ABC中,![]() ,∴
,∴![]() ,∴BC=
,∴BC=![]() ,∴AC=
,∴AC=![]() ,∴S△ABC=
,∴S△ABC=![]() ACBC=5.
ACBC=5.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?