题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC形内一点,且∠APB=∠APC=135°.
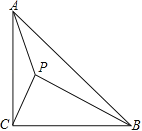
(1)求证:△CPA∽△APB;
(2)试求tan∠PCB的值.
【答案】(1)见解析 (2)2.
【解析】
试题(1)根据∠PBA+∠PAB=45°和∠PAC+∠PAB=45°得出∠PAC=∠PBA,再根据已知条件∠APB=∠APC得出三角形相似;(2)根据等腰直角三角形的性质得出CA和AB的比值,设CP=k,则PB=2k,然后根据∠BPC=90°求出∠PCB的正切值.
试题解析:(1)∵在△ABC中,∠ACB=90°,AC=BC,∴∠BAC=45°,即∠PAC+∠PAB=45°,
又在△APB中,∠APB=135°, ∴∠PBA+∠PAB=45°, ∴∠PAC=∠PBA,
又∠APB=∠APC, ∴△CPA∽△APB.
(2)∵△ABC是等腰直角三角形,
∴![]() , 又∵△CPA∽△APB, ∴
, 又∵△CPA∽△APB, ∴![]() ,
,
令CP=k,则![]() ,
,
又在△BCP中,∠BPC=360°﹣∠APC﹣∠APB=90°, ∴![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由