题目内容
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场．现由甲、乙两个工厂来加工生产．已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍，并且加工生产240件新产品甲工厂比乙工厂少用4天．
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品？
(2)若甲工厂每天的加工生产成本为3万元，乙工厂每天的加工生产成本为2.4万元，要使这批新产品的加工生产总成本不超过60万元，至少应安排甲工厂加工生产多少天？
【答案】(1)甲工厂每天可以加工生产30件新产品，乙工厂每天可以加工生产20件新产品；(2)至少应安排甲工厂加工生产12天．
【解析】
（1）设乙工厂每天可以加工生产x件新产品，则甲工厂每天可以加工生产1.5x件新产品，根据工作时间=工作总量÷工作效率结合加工生产240件新产品甲工厂比乙工厂少用4天，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）设安排甲工厂加工生产m天，则安排乙工厂加工生产（28-1.5m）天，根据总费用=3×甲工厂加工生产的天数+2.4×乙工厂加工生产的天数结合总成本不超过60万元，即可得出关于m的一元一次不等式，解之取其最小值即可得出结论．
(1)设乙工厂每天可以加工生产x件新产品，则甲工厂每天可以加工生产1.5x件新产品，
依题意，得：
，
解得：x＝20，
经检验，x＝20是原分式方程的解，且符合题意，
∴1.5x＝30．
答：甲工厂每天可以加工生产30件新产品，乙工厂每天可以加工生产20件新产品．
(2)设安排甲工厂加工生产m天，则安排乙工厂加工生产(28﹣1.5m)天，
依题意，得：3m+2.4(28﹣1.5m)≤60，
解得：m≥12．
答：至少应安排甲工厂加工生产12天．
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行一次测试（满分50分，成绩均记为整数分），并按测试成绩m（单位：分）分类：A类（45＜m≤50），B类（40＜m≤45），C类（35＜m≤40），D类（m≤35）绘制出如图所示的不完整条形统计图，请根据图中信息解答下列问题：
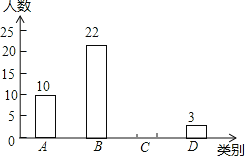
（1）a＝ ，b＝ ，c＝ ；
成绩等级 | 人数 | 所占百分比 |
A类（45 | 10 | 20% |
B类 | 22 | 44% |
C类 | a | b |
D类 | c |
（2）补全条形统计图；
（3）若该校九年级男生有600名，D类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？