题目内容
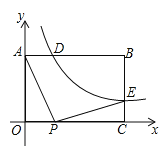
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图像与矩形两边AB、BC分别交于点D、点E,且
)的图像与矩形两边AB、BC分别交于点D、点E,且![]() .
.
(1)求点D的坐标和![]() 的值;
的值;
(2)求证:![]() ;
;
(3)若点![]() 是线段
是线段![]() 上的一个动点,是否存在点
上的一个动点,是否存在点![]() ,使
,使![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,4;(2)见解析;(3)存在点
,4;(2)见解析;(3)存在点![]() ,
,![]() 或
或![]() .
.
【解析】
(1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的长,然后求得点D的坐标,即可求得k的值,继而求得点E的坐标;
(2)由E点在反比例函数![]() 图像上,可求E点坐标,进而求出EC的长即可求证.
图像上,可求E点坐标,进而求出EC的长即可求证.
(3)首先假设存在要求的点P坐标为(m,0),OP=m,CP=4-m,由∠APE=90°,易证得△AOP∽△PCE,然后由相似三角形的对应边成比例,求得m的值,继而求得此时点P的坐标.
解:(1)在矩形![]() 中,
中,![]() 轴,且
轴,且![]() ,
,

∴点![]() 的纵坐标为3.
的纵坐标为3.
∵![]() ,且
,且![]() ,
,
![]() ,
,
∴![]() .
.
∴点![]() 在反比例函数
在反比例函数![]() 图像上,
图像上,
∴![]() .
.
(2)证:∵![]() 在
在![]() 上,
上,
∴![]() 横坐标为4,
横坐标为4,
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)存在点![]() ,使
,使![]() ,其过程是:
,其过程是:
设![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,即
,即![]() .解得
.解得![]() 或
或![]() .
.
![]() 或
或![]() .
.

练习册系列答案
相关题目