题目内容
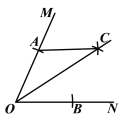
【题目】如图，点O在∠APB的平分线上，⊙O与PA相切于点C．
（1）求证：直线PB与⊙O相切；
（2）PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．
【答案】(1)证明见解析；（2）
【解析】试题（1）连接OC，作OD⊥PB于D点．证明OD=OC即可．根据角的平分线性质易证；
（2）设PO交⊙O于F，连接CF．根据勾股定理得PO=5，则PE=8．证明△PCF∽△PEC，得CF：CE=PC：PE=1：2．根据勾股定理求解CE．
试题解析：（1）证明：连接OC，作OD⊥PB于D点．
∵⊙O与PA相切于点C， ∴OC⊥PA．
（2）解：设PO交⊙O于F，连接CF．
∵OC=3，PC=4，∴PO=5，PE=8．
∵⊙O与PA相切于点C， ∴∠PCF=∠E．
又∵∠CPF=∠EPC， ∴△PCF∽△PEC，
∴CF：CE=PC：PE=4：8=1：2．
∵EF是直径， ∴∠ECF=90°．
设CF=x，则EC=2x．
则x2+（2x）2=62， 解得x=
．
则EC=2x=
．
练习册系列答案
相关题目
