题目内容
如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F.求证：△BED≌△CFD.
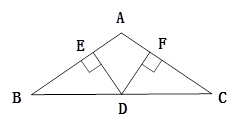
证明见解析.
试题分析：利用等腰三角形的性质，可得到∠B=∠C，D又是BC的中点，利用AAS，可证出：△BED≌△CFD．
试题解析：∵DE⊥AB，DF⊥AC，
∴∠BED=∠CFD=90°．
∵AB=AC，
∴∠B=∠C．
∵D是BC的中点，
∴BD=CD．
∴△BED≌△CFD．
考点: 1.全等三角形的判定与性质；2.等腰三角形的性质.
练习册系列答案
相关题目
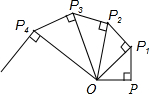
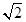；再过P1作P1P2⊥OP1且P1P2=1，得OP2=
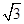；又过P2作P2P3⊥OP2且P2P3=1，得OP3=2；…依此法继续作下去，得OP2012= ．
