题目内容
【题目】[阅读理解]
我们知道:
，那么
结果等于多少呢?
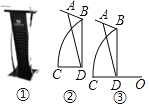
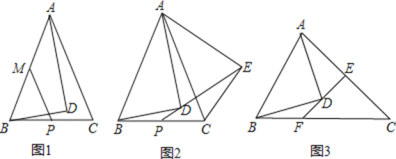
在图1所示的等边三角形数阵中，第
行的一个小等边三角形中的数为，即
第
行的三个小等边三角形中的数的和是
即
; ．．第
行的
个小等边三角形中的数的和是
个，即
，该等边三角形数阵中共有
小等边三角形，所有小等边三角形数的和为．
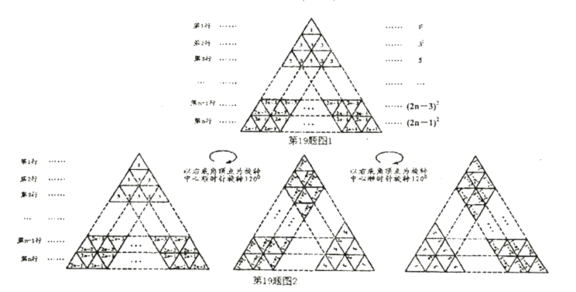
[规律探究]
以图1中的等边三角形数阵的右底角顶点为旋转中心顺时针旋转
再把旋转后的图形按同样的方法可得如图2所示的三角形数阵，观察这三个等边三角形数阵各行同一位置的小等边三角形中的数，发现位于奇数位置的三个数(如第
行的第个小三角形中的数分别为
的和为
;发现位于偶数位置的三个数(如第行的第个小三角形中的数分别为
的和为
;而每个等边三角形数阵中，由于位于奇数位置的数比位于偶数位置的数多个，则位于偶数位置的数有_
个
因此，
[解决问题]根据以上发现，计算:
【答案】[规律探究]
，
，
，
；[解决问题]
【解析】
[规律探究] 设每个等边三角形数阵中位于偶数位置的数有x个，根据题意列出方程即可求出x的值，从而求出每个等边三角形数阵中位于奇数位置的数的个数，再根据题意，即可求出这三个等边三角形数阵所有数的总和，即可求出最终结论；
[解决问题] 令2n－1=2019，即可求出n的值，然后代入[规律探究]的公式即可求出结论．
解：[规律探究]设每个等边三角形数阵中位于偶数位置的数有x个，
由题意可得x＋（x＋n）=n2
解得：x=，
则每个等边三角形数阵中位于奇数位置的数有＋n=
∴由此可得，这三个等边三角形数阵所有数的总和为: 
（4n＋1）×＋（4n－1）×=
∴
故答案为：，，，；
[解决问题] 令2n－1=2019
解得：n=1010
=
＝
练习册系列答案
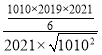
阅读快车系列答案
相关题目
