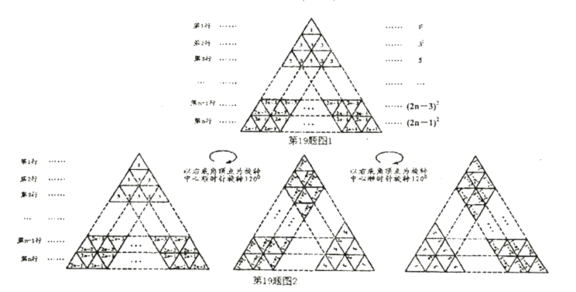
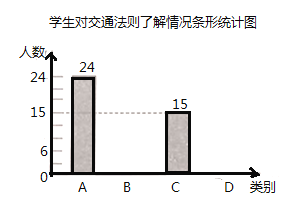
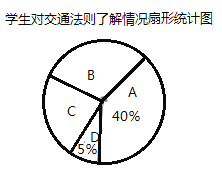
��Ŀ����
����Ŀ������һ��������������������ͼ���ϴ���һ���㣬���ĺᡢ��������ȣ���ô���������ú����IJ���㣮
��1��һ�κ���![]() �IJ���������Ϊ______��
�IJ���������Ϊ______��
��2�����κ���![]() �����������ֱ�Ϊ��
�����������ֱ�Ϊ��![]() ��
��![]() ��
��![]() ����ࣩ������
����ࣩ������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90���õ���
˳ʱ����ת90���õ���![]() �����
�����![]() �����꣮
�����꣮
��3����֪���κ���![]() ����������������Ϊ
����������������Ϊ![]() ��
��
����![]() ��ֵ��
��ֵ��
����ͼ����������![]() ���߶�
���߶�![]() Χ�ɵķ��ͼ�μ���
Χ�ɵķ��ͼ�μ���![]() ����
����![]() Ϊһ�κ���
Ϊһ�κ���![]() �IJ���㣬���߶�
�IJ���㣬���߶�![]() Ϊ��������������
��������������![]() ����
����![]() ������ֻ��һ�����ڷ��ͼ��
������ֻ��һ�����ڷ��ͼ��![]() ���ڲ����������߽磩ʱ�����
���ڲ����������߽磩ʱ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1����1��1������2��![]() ��
��![]() ����3����
����3����![]() ����
����![]() ��
��![]()
��������
��1������һ�κ���y��3x��2��y��x��ɷ����飬��֮���ɵó����ۣ�
��2���������κ���y��x2��3x+1��y��x��ɷ����飬��֮���ɵó���P��Q�����꣬�ɵ�P��Q��ֱ��y��x�ϣ��ɵó���PQRΪ����ֱ�������Σ�����P��PP���QR������Ϊ��P�䣬���ݵ���ֱ�������ε����ʼ��ɵó���R�����ꣻ
��3�������ݵ�A��B�����꣬���ô���ϵ�����������a��b��ֵ��
������һ�κ���y����![]() x+m��y��x�ɷ����飬��֮���ɵó���C�����꣬���������ε����ʿɵó���D��E�����꣬��ֻ�е�D��ͼ��M���ڲ���ֻ�е�E��ͼ��M���ڲ���������ҳ�����m�IJ���ʽ�飬��֮���ɵó����ۣ�����ֻд�𰸲�д���̵Ŀ���ֱ�Ӵ����D��E�����꣬���ü����ҳ�m��ȡֵ��Χ����
x+m��y��x�ɷ����飬��֮���ɵó���C�����꣬���������ε����ʿɵó���D��E�����꣬��ֻ�е�D��ͼ��M���ڲ���ֻ�е�E��ͼ��M���ڲ���������ҳ�����m�IJ���ʽ�飬��֮���ɵó����ۣ�����ֻд�𰸲�д���̵Ŀ���ֱ�Ӵ����D��E�����꣬���ü����ҳ�m��ȡֵ��Χ����
�⣺��1����������ã�![]() ��
��
��ã�![]() ��
��
��һ�κ���y��3x��2�IJ����������Ϊ��1��1����
��2����������ã�![]() ��
��
��ã�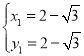 ��
��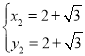 ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ߵ�P��Q��ֱ��y��x�ϣ�
���QPR��45�㣬
���PQRΪ����ֱ�������Σ�
����P��PP���QR������Ϊ��P�䣬��ͼ1��ʾ��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��3�����߶��κ���y��ax2+bx��3����������������ΪA����1����1����B��3��3����
![]()
![]() ��
��
��ã�![]() ��
��
��![]()
 ����ã�
����ã�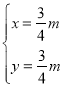 ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��
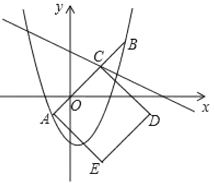
���ı���ACDEΪ�����Σ���A��C��ֱ��y��x�ϣ�A����1����1����
![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ֻ�е�![]() ��ͼ��
��ͼ��![]() ���ڲ�ʱ����
���ڲ�ʱ���� ��
��
���![]() ��
��
��ֻ�е�![]() ��ͼ��
��ͼ��![]() ���ڲ�ʱ����
���ڲ�ʱ����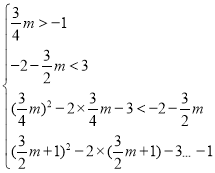 ��
��
��ã�![]() ��
��
����������![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��![]() ��
��