题目内容
【题目】如图，在△ABC中，AB=AC，∠BAC=90°，AH⊥BC于点H，过点C作CD⊥AC，连接AD，点M为AC上一点，且AM=CD，连接BM交AH于点N，交AD于点E．
（1）若AB=3，AD=
，求△BMC的面积；
（2）点E为AD的中点时，求证：AD=
BN ．
【答案】（1）3；（2）证明见解析．
【解析】试题分析：（1）只要证明△ABM≌△CAD，推出BM=AD=
，推出AM=1，推出CM=CA﹣AM=2，根据S△BCM=
CMBA，计算即可；
（2）如图2中，连接EC、CN，作EQ⊥BC于Q，EP⊥BA于P．想办法证明△ENC是等腰直角三角形即可解决问题．
试题解析：解：（1）如图1中，在△ABM和△CAD中，∵AB=AC，∠BAM=∠ACD=90°，AM=CD，∴△ABM≌△CAD，∴BM=AD=
，∴AM=
=1，∴CM=CA﹣AM=2，∴S△BCM=
CMBA=
×23=3．
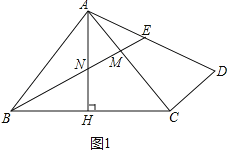
（2）如图2中，连接EC、CN，作EQ⊥BC于Q，EP⊥BA于P．
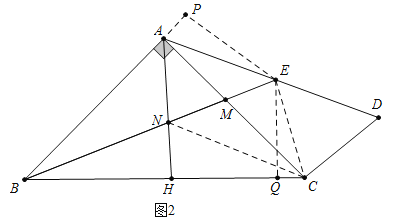
∵AE=ED，∠ACD=90°，∴AE=CE=ED，∴∠EAC=∠ECA，∵△ABM≌△CAD，∴∠ABM=∠CAD，∴∠ABM=∠MCE，∵∠AMB=∠EMC，∴∠CEM=∠BAM=90°，∵△ABM∽△ECM，∴ 
，∴
，∵∠AME=∠BMC，∴△AME∽△BMC，∴∠AEM=∠ACB=45°，∴∠AEC=135°，易知∠PEQ=135°，∴∠PEQ=∠AEC，∴∠AEQ=∠EQC，∵∠P=∠EQC=90°，∴△EPA≌△EQC，∴EP=EQ，∵EP⊥BP，EQ⊥BC
∴BE平分∠ABC，∴∠NBC=∠ABN=22.5°，∵AH垂直平分BC，∴NB=NC，∴∠NCB=∠NBC=22.5°，∴∠ENC=∠NBC+∠NCB=45°，∴△ENC的等腰直角三角形，∴NC=
EC，∴AD=2EC，∴2NC=
AD，∴AD=
NC，∵BN=NC，∴AD=
BN．
