ƒøƒ⁄»ð
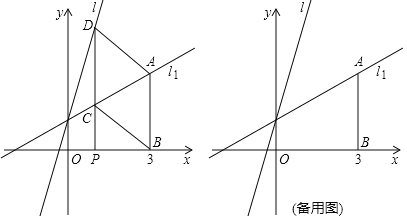
°æƒø°ø»ÁÕº£®1£©£¨π´¬∑…œ”–A°¢B°¢C»˝∏ˆ≥µ’棨“ª¡æ∆˚≥µ¥”A’æ“‘ÀŸ∂»v1‘»ÀŸ ªœÚB’棨µΩ¥ÔB’æ∫Û≤ªÕ£¡Ù£¨“‘ÀŸ∂»v2‘»ÀŸ ªœÚC’棨∆˚≥µ–– ª¬∑≥Ãy£®«ß√◊£©”Ζ– ª ±º‰x£®–° ±£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ»ÁÕº£®2£©À˘ æ£Æ

£®1£©µ±∆˚≥µ‘⁄A°¢B¡Ω’æ÷ƺ‰‘»ÀŸ–– ª ±£¨«Ûy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ωº∞◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®2£©«Û≥ˆv2µƒ÷µ£ª
£®3£©»Ù∆˚≥µ‘⁄ƒ≥“ª∂Œ¬∑≥Ã⁄∏’∫√”√50∑÷÷”–– ª¡À90«ß√◊£¨«Û’‚∂Œ¬∑≥Ãø™ º ±xµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©y=100x£¨£®0£ºx£º3£©£ª£®2£©120«ß√◊/–° ±£ª£®3£©’‚∂Œ¬∑≥Ãø™ º ±xµƒ÷µ «2.5–° ±£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æð∫Ø ˝ÕºœÛ…Ë≥ˆ“ª¥Œ∫Ø ˝Ω‚Œˆ Ω£¨‘À”√¥˝∂®œµ ˝∑®«Û≥ˆΩ‚Œˆ Ωº¥ø…£ª
£®2£©∏˘æðæý¿Î°¬ ±º‰=ÀŸ∂»º∆À„£ª
£®3£©…Ë∆˚≥µ‘⁄A°¢B¡Ω’æ÷ƺ‰‘»ÀŸ–– ªx–° ±£¨∏˘æð“‚¡–≥ˆ∑Ω≥ã¨Ω‚∑Ω≥ú¥ø…£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©∏˘æðÕºœÛø……Ë∆˚≥µ‘⁄A°¢B¡Ω’æ÷ƺ‰‘»ÀŸ–– ª ±£¨y”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™y=kx£¨
°þÕºœÛæ≠π˝£®1£¨100£©£¨
°ýk=100£¨
°ýy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™y=100x£¨£®0£ºx£º3£©£ª
£®2£©µ±y=300 ±£¨x=3£¨
4©Å3=1–° ±£¨420©Å300=120«ß√◊£¨
°ýv2=120«ß√◊/–° ±£ª
£®3£©…Ë∆˚≥µ‘⁄A°¢B¡Ω’æ÷ƺ‰‘»ÀŸ–– ªx–° ±£¨‘Ú‘⁄∆˚≥µ‘⁄B°¢C¡Ω’æ÷ƺ‰‘»ÀŸ–– ª£®![]() ©Åx£©–° ±£¨
©Åx£©–° ±£¨
”…“‚µ√£¨100x+120£®![]() ©Åx£©=90£¨
©Åx£©=90£¨
Ω‚µ√x=0.5£¨
3©Å0.5=2.5–° ±£Æ
¥£∫’‚∂Œ¬∑≥Ãø™ º ±xµƒ÷µ «2.5–° ±£Æ