题目内容
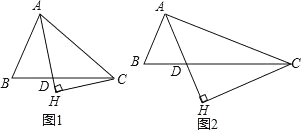
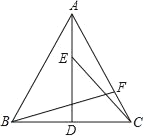
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )
A. 112.5°B. 105°C. 90°D. 82.5°
【答案】B
【解析】
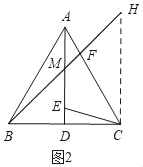
如图,作辅助线,构建全等三角形,证明△AEC≌△CFH,得CE=FH,将CE转化为FH,与BF在同一个三角形中,根据两点之间线段最短,确定点F的位置,即F为AC与BH的交点时,BF+CE的值最小,求出此时∠AFB=105°.
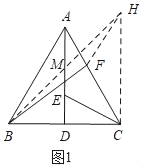
解:如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,
∵△ABC是等边三角形,AD⊥BC,
∴AC=BC,∠DAC=30°,
∴AC=CH,
∵∠BCH=90°,∠ACB=60°,
∴∠ACH=90°﹣60°=30°,
∴∠DAC=∠ACH=30°,
∵AE=CF,
∴△AEC≌△CFH,
∴CE=FH,BF+CE=BF+FH,
∴当F为AC与BH的交点时,如图2,BF+CE的值最小,
此时∠FBC=45°,∠FCB=60°,
∴∠AFB=105°,
故选:B.

练习册系列答案
相关题目