题目内容
【题目】如图,已知抛物线y=x![]() -ax+a
-ax+a![]() -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
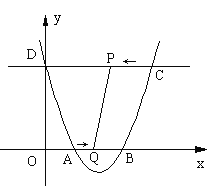
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
【答案】(1)8(2)![]() (3)
(3)![]() (4)
(4)![]()
【解析】解:(1)∵抛物线y=x![]() -ax+a
-ax+a![]() -4a-4经过点(0,8)
-4a-4经过点(0,8)
∴a![]() -4a-4=8
-4a-4=8
解得:a![]() =6,a
=6,a![]() =-2(不合题意,舍去)
=-2(不合题意,舍去)
∴a的值为6
(2)由(1)可得抛物线的解析式为
y=x![]() -6x+8
-6x+8
当y=0时,x![]() -6x+8=0
-6x+8=0
解得:x![]() =2,x
=2,x![]() =4
=4
∴A点坐标为(2,0),B点坐标为(4,0)
当y=8时,
x=0或x=6
∴D点的坐标为(0,8),C点坐标为(6,8)
DP=6-2t,OQ=2+t
当四边形OQPD为矩形时,DP=OQ
2+t=6-2t,t=![]() ,OQ=2+
,OQ=2+![]() =
=![]()
S=8×![]() =
=![]()
即矩形OQPD的面积为![]()
(3)四边形PQBC的面积为![]() ,当此四边形的面积为14时,
,当此四边形的面积为14时,
![]() (2-t+2t)×8=14
(2-t+2t)×8=14
解得t=![]() (秒)
(秒)
当t=![]() 时,四边形PQBC的面积为14
时,四边形PQBC的面积为14
(4)过点P作PE⊥AB于E,连接PB,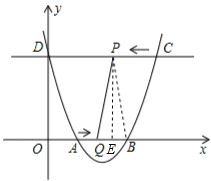
当QE=BE时,△PBQ是等腰三角形,
∵CP=2t,
∴DP=6-2t,
∴BE=OB-PD=4-(6-2t)=2t-2,
∵OQ=2+t,
∴QE=PD-OQ=6-2t-(2+t)=4-3t,
∴4-3t=2t-2,
解得:t= ![]() ,
,
∴当t= ![]() 时,△PBQ是等腰三角形
时,△PBQ是等腰三角形
t=![]() 时,PBQ是等腰三角形.
时,PBQ是等腰三角形.
(1)把点D(0,8)代入抛物线y=x2-ax+a2-4a-4解方程即可解答;
(2)利用(1)中求得的抛物线,求得点A、B、C、D四点坐标,再利用矩形的判定与性质解得即可;
(3)利用梯形的面积计算方法解决问题;
(4)只考虑PQ=PB,其他不符合实际情况,即可找到问题的答案

 天天向上口算本系列答案
天天向上口算本系列答案【题目】某学校对学生的暑假参加志愿服务时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).

请结合以上信息解答下列问题
(1)求a、m、n的值.
(2)补全“人数分组统计图①中C组的人数和图②A组和B组的比例值”.
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在30≤x<40的范围的学生人数.
分组统计表
组别 | 志愿服务时间 x(时) | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 40 |
C | 20≤x<30 | m |
D | 30≤x<40 | n |
E | x≥40 | 16 |