题目内容
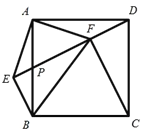
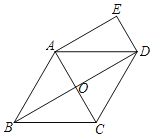
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形;
(2)证明△ABC是等边三角形,得出OA=1,由勾股定理得出OB=![]() ,由菱形的性质得出OD=OB=
,由菱形的性质得出OD=OB=![]() ,即可求出四边形AODE的面积.
,即可求出四边形AODE的面积.
(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC=2,
∴△ABC是等边三角形,
∴OA=![]() ×2=1,
×2=1,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目