Question

【题目】如图AM∥BN，C是BN上一点， BD平分∠ABN且过AC的中点O，交AM于点D，DE⊥BD，交BN于点E．

（1）求证：△ADO≌△CBO．

（2）求证：四边形ABCD是菱形．

（3）若DE = AB = 2，求菱形ABCD的面积．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）由ASA即可得出结论；

（2）先证明四边形ABCD是平行四边形，再证明AD＝AB，即可得出结论；

（3）由菱形的性质得出AC⊥BD，证明四边形ACED是平行四边形，得出AC＝DE＝2，AD＝EC，由菱形的性质得出EC＝CB＝AB＝2，得出EB＝4，由勾股定理得BD═，即可得出答案．

（1）∵点O是AC的中点，

∴AO＝CO，

∵AM∥BN，

∴∠DAC＝∠ACB，

在△AOD和△COB中，

，

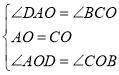∴△ADO≌△CBO（ASA）；

（2）由（1）得△ADO≌△CBO，

∴AD＝CB，

又∵AM∥BN，

∴四边形ABCD是平行四边形，

∵AM∥BN，

∴∠ADB＝∠CBD，

∵BD平分∠ABN，

∴∠ABD＝∠CBD，

∴∠ABD＝∠ADB，

∴AD＝AB，

∴平行四边形ABCD是菱形；

（3）由（2）得四边形ABCD是菱形，

∴AC⊥BD，AD＝CB，

又DE⊥BD，

∴AC∥DE，

∵AM∥BN，

∴四边形ACED是平行四边形，

∴AC＝DE＝2，AD＝EC，

∴EC＝CB，

∵四边形ABCD是菱形，

∴EC＝CB＝AB＝2，

∴EB＝4，

在Rt△DEB中，由勾股定理得BD＝＝，

∴．