题目内容
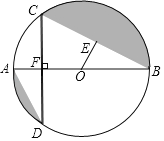
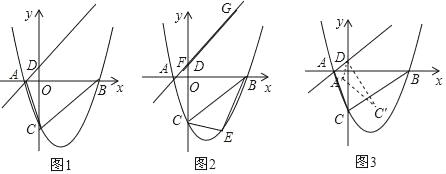
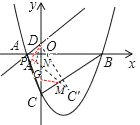
【题目】如图1,抛物线y=![]() x2﹣
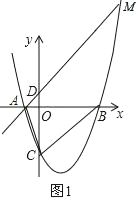
x2﹣![]() x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为
x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为![]() ,直线AM与y轴交于点D,连接BC、AC.
,直线AM与y轴交于点D,连接BC、AC.
(1)求直线AD和BC的解折式;
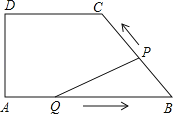
(2)如图2,E为直线BC下方的抛物线上一点,当△BCE的面积最大时,一线段FG=4![]() (点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
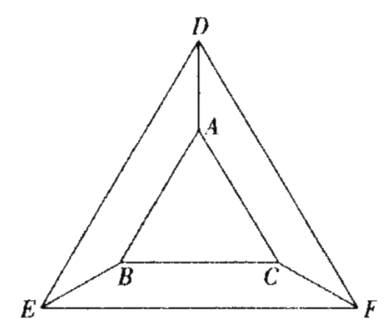
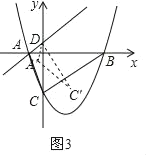
(3)如图3,将△DAC绕点D逆时针旋转角度α(0°<α<180°),记旋转中的三角形为△DA′C′,若直线A′C′分别与直线BC、y轴交于M、N,当△CMN是等腰三角形时,请直接写出CM的长度.
【答案】(1)y=x+1,y=![]() x﹣3;(2)F(
x﹣3;(2)F(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)令y=0,得x1=-1,x2=4,A(-1,0),B(4,0),令x=0,得C(0,-3),令x=![]() ,得y=
,得y=![]() ,M(
,M(![]() ,
,![]() ),待定系数法可求直线AD、BC的解析式;
),待定系数法可求直线AD、BC的解析式;
(2)点F是直线BC下方抛物线上的动点,△FBC面积最大值可以转化为求二次函数最大值问题,设点F横坐标为t,则可以将△FBC面积表示成t的二次函数,再应用配方法将二次函数化成顶点式,就可以求出△FBC面积最大时,F的坐标;四边形BEFG周长的最大值实际上就是求EF+BG的最大值,通过轴对称求线段和的最小值方法求解;
(3)△CMN是等腰三角形,必须分三种不同情况讨论:①CM=CN,②CM=MN,③CN=MN.
解:(1)在抛物线y=![]() 中,令x=0,得y=﹣3,
中,令x=0,得y=﹣3,
∴C(0,﹣3),
令y=0,得![]() ,解得x1=﹣1,x2=4,
,解得x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
令x=![]() ,得y=
,得y=![]() =
=![]() ,
,
∴M(![]() ,
,![]() ),
),
设直线AD的解析式为y=k1x+b1,将A(﹣1,0),M(![]() ,
,![]() )代入得
)代入得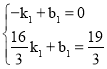 ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1.
设直线BC的解析式为y=k2x+b2,将B(4,0),C(0,﹣3)代入,得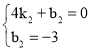 ,
,
解得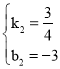 ,
,
∴直线BC的解析式为y=![]() x﹣3;
x﹣3;
(2)如图2,过点E作EH∥y轴交BC于H,

设E(t,![]() ),H(t,
),H(t,![]() ),
),
∴HE=![]() =
=![]()
∴![]() =
=![]() =
=![]() =
=![]()
∵![]() <0,
<0,
∴当t=2时,S△BCE的最大值=6,此时E(2,![]() ),
),
作点B关于直线y=x+1的对称点B1,连接B1G,过点F作B2F∥B1G,且B2F=B1G,
∴B1(﹣1,5),
∵FG=4![]() ,且FG在直线y=x+1上,
,且FG在直线y=x+1上,
∴F可以看作是G向左平移4个单位,向下平移4个单位后的对应点,
∴B2(﹣5,1),
当B2、F、E三点在同一直线上时,BEFG周长最小,设直线B2E解析式为y=mx+n,将B2(﹣5,1),E(2,![]() )分别代入,得
)分别代入,得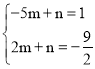 ,
,
解得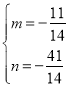 ,
,
∴直线B2E解析式为y=![]() ,
,
联立方程组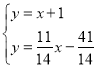 ,
,
解得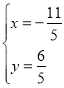 .
.
∴F(![]() ,
,![]() ).
).
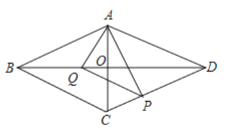
(3)如图,分三种情况:
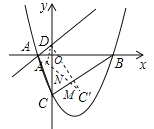
在![]() 中,令
中,令![]() ,则
,则![]()
![]()
![]()
![]()
![]() ,
,
设AC边上的高为h,根据等面积法得,![]()
![]()
![]() 且OB⊥OC,
且OB⊥OC,
![]()
①CM=MN时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P
![]()
∴设![]() ,则
,则![]() ,
,
由勾股定理得,![]() ,
,
![]()
![]()
![]() ,即
,即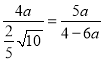
解得,![]() ,
,![]() (舍去)
(舍去)
![]()
②当![]() 时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P
时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P

![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
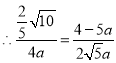 ,解得:
,解得:![]() (舍去),
(舍去),![]() ,
,
![]() ;
;
③当![]() 时,如图,作
时,如图,作![]() ,
,![]() ,
,
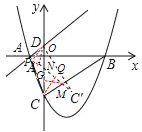
![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即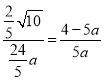 ,解得,
,解得,![]() (舍去),
(舍去),![]()
![]() ;
;
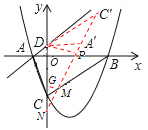
④当![]() 时,过M作
时,过M作![]() ,过点D作DP⊥MN于点P
,过点D作DP⊥MN于点P
![]()
设![]() ,则
,则![]()
![]()
![]()
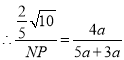
![]()
在![]() 中,
中,![]()
![]()
解得,![]() (舍去)
(舍去)
![]() .
.
综上,CM的长为![]() ,
,![]() ,
,![]() 或
或![]() .
.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别 | 平均数 | 中位数 | 众数 | 方差 |
A组 | 89 | 89 | b | c |
B组 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .