题目内容
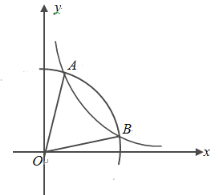
【题目】如图,矩形ABCD中,AD>AB,连接AC,将线段AC绕点A顺时针旋转90得到线段AE,平移线段AE得到线段DF(点A与点D对应,点E与点F对应),连接BF,分别交直线AD,AC于点G,M,连接EF.
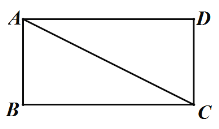
(1) 依题意补全图形;
(2) 求证:EG⊥AD;
(3) 连接EC,交BF于点N,若AB=2,BC=4,设MB=a,NF=b,试比较![]() 与
与![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
【答案】(1)见解析;(2)见解析;(3)![]() <
<![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据题目要求作出图形即可;
(2)连EF,EG,延长AB交EF于点H,先依据矩形与平行线的性质,等角的余角相等,旋转的性质,得到![]() ≌
≌![]() (AAS),依据全等的性质及等量代换可得
(AAS),依据全等的性质及等量代换可得![]() ,结合依据相似的判定与性质,得到
,结合依据相似的判定与性质,得到![]() ,再依据SAS可证明
,再依据SAS可证明![]() ≌
≌![]() ,依据全等的性质得到
,依据全等的性质得到![]() ,即EG⊥AD;
,即EG⊥AD;
(3)依据勾股定理求出![]() ,依据平行线分线段成比例可分别证
,依据平行线分线段成比例可分别证![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,依据相似三角形的性质得到
,依据相似三角形的性质得到![]() 、
、![]() 、
、![]() 、
、![]() ,即可求出
,即可求出![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.
解:(1)补全图形如下:
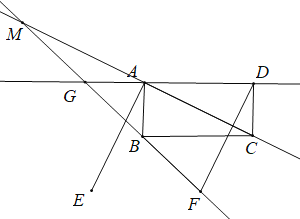
(2)连EF,EG,延长AB交EF于点H,设![]() ,
,![]() ,
,
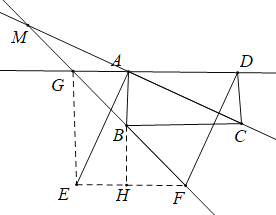
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵矩形ABCD,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,
∴EG⊥AD;
(3) 当AB=2,BC=4,MB=a,NF=b时,![]() <
<![]() ,理由如下:
,理由如下:
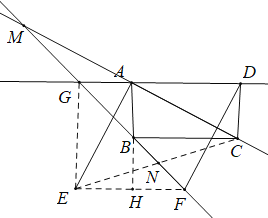
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵![]()
![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目