题目内容
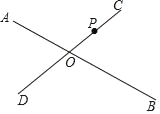
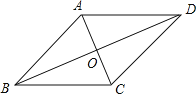
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 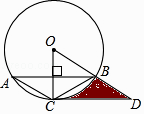
【答案】2 ![]() ﹣
﹣ ![]() π
π
【解析】解:∵OC⊥AB,∠A=∠BCD=30°,AC=2, ∴∠O=60°, ![]() =
= ![]() ,
,
∴AC=BC=6,
∴∠ABC=∠A=30°,
∴∠OCB=60°,
∴∠OCD=90°,
∴OC=BC=2,
∴CD= ![]() OC=2
OC=2 ![]() ,
,
∴线段CD和线段BD所围成图形的阴影部分的面积=S△OCD﹣S扇形BOC﹣ ![]() 2×2
2×2 ![]() ﹣
﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() π,
π,
所以答案是:2 ![]() ﹣
﹣ ![]() π.
π.
【考点精析】根据题目的已知条件,利用垂径定理和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目