Question

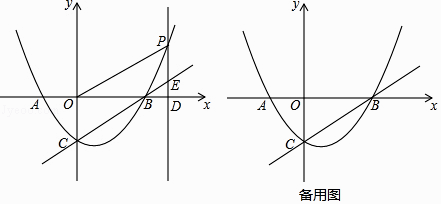
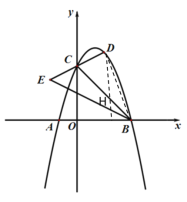
【题目】如图，抛物线y=﹣x2+bx+c（a≠0）与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C，点D的横坐标为m（0＜m＜3），连结DC并延长至E，使得CE=CD，连结BE，BC．

（1）求抛物线的解析式；

（2）用含m的代数式表示点E的坐标，并求出点E纵坐标的范围；

（3）求△BCE的面积最大值．

Answer 1

【答案】（1）y=﹣x2+2x+3．（2）2≤Ey＜6．（3）当m=1.5时，S△BCE有最大值，S△BCE的最大值=．

【解析】

(1) 1)把A、B两点代入抛物线解析式即可;(2)设，利用求线段中点的公式列出关于m的方程组，再利用0＜m＜3即可求解;(3) 连结BD，过点D作x轴的垂线交BC于点H,由，设出点D的坐标，进而求出点H的坐标，利用三角形的面积公式求出，再利用公式求二次函数的最值即可.

(1)∵抛物线 过点A（1，0）和B（3，0）

（2）∵

∴点C为线段DE中点

设点E（a,b）

∵0＜m＜3,

∴当m=1时，纵坐标最小值为2

当m=3时，最大值为6

∴点E纵坐标的范围为

（3）连结BD，过点D作x轴的垂线交BC于点H

∵CE=CD

∴H（m，-m+3）

∴

当m=1.5时，

.