题目内容
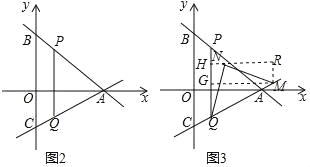
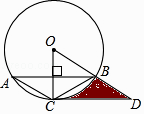
【题目】如图1，平面直角坐标系中，直线AB：y=﹣
x+b交x轴于点A(8，0)，交y轴正半轴于点B.
(1)求点B的坐标；
(2)如图2，直线AC交y轴负半轴于点C，AB=BC，P为线段AB上一点，过点P作y轴的平行线交直线AC于点Q，设点P的横坐标为t，线段PQ的长为d，求d与t之间的函数关系式；
(3)在(2)的条件下，M为CA延长线上一点，且AM=CQ，在直线AC上方的直线AB上是否存在点N，使△QMN是以QM为斜边的等腰直角三角形？若存在，请求出点N的坐标及PN的长度；若不存在，请说明理由.
【答案】(1) B(0，6)；(2) d=﹣
t+10；(3)见解析.
【解析】(1)把A(8，0)代入y=﹣
x+b，可求解析式，再求B的坐标；（2）先求点C(0，﹣4)，再求直线AC解析式，可设点P(t，﹣t+6)，Q(t，
t﹣4)，所以d=(﹣t+6)﹣(t﹣4)；过点M作MG⊥PQ于G，证△OAC≌△GMQ，得QG=OC=4，GM=OA=8；过点N作NH⊥PQ于H，过点M作MR⊥NH于点R，得四边形GHRM是矩形，得HR=GM=8；设GH=RM=k，由△HNQ≌△RMN，得HN=RM=k，NR=QH=4+k，由HR=HN+NR，得k+4+k=8，可得GH=NH=RM=2，HQ=6，由Q(t，t﹣4)，得N(t+2，t﹣4+6)，代入y=﹣x+6，得t+2=﹣(t+2)+6，求出t=2，再求P(2，
)，N(4，3)，可得PH=
，NH=2，最后PN=
.
解：(1)∵y=﹣x+b交x轴于点A(8，0)，
∴0=﹣×8+b，b=6，
∴直线AB解析式为y=﹣x+6，令x=0，y=6，B(0，6)；
(2)∵A(8，0)，B(0，6)，
∴OA=8，OB=6，
∵∠AOB=90°，
∴AB=10=BC，
∴OC=4，
∴点C(0，﹣4)，设直线AC解析式为y=kx+b’，
∴
，
∴
,
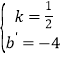∴直线AC解析式为y=x﹣4，
∵P在直线y=﹣x+6上，
∴可设点P(t，﹣t+6)，
∵PQ∥y轴，且点Q在y=x﹣4 上，
∴Q(t， t﹣4)，
∴d=(﹣t+6)﹣(t﹣4)=﹣t+10；
(3)过点M作MG⊥PQ于G，
∴∠QGM=90°=∠COA，
∵PQ∥y轴，
∴∠OCA=∠GQM，
∵CQ=AM，
∴AC=QM，在△OAC与△GMQ中，
，
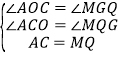∴△OAC≌△GMQ，
∴QG=OC=4，GM=OA=8，过点N作NH⊥PQ于H，过点M作MR⊥NH于点R，
∴∠MGH=∠RHG=∠MRH=90°，
∴四边形GHRM是矩形，
∴HR=GM=8，可设GH=RM=k，
∵△MNQ是等腰直角三角形，
∴∠QMN=90°，NQ=NM，
∴∠HNQ+∠HQN=90°，
∴∠HNQ+∠RNM=90°，
∴∠RNM=∠HQN，
∴△HNQ≌△RMN，
∴HN=RM=k，NR=QH=4+k，
∵HR=HN+NR，
∴k+4+k=8，
∴k=2，
∴GH=NH=RM=2，
∴HQ=6，
∵Q(t，t﹣4)，
∴N(t+2，t﹣4+6)即 N(t+2，t+2)
∵N在直线AB：y=﹣x+6上，
∴t+2=﹣(t+2)+6，
∴t=2，
∴P(2，)，N(4，3)，
∴PH=，NH=2，
∴PN=
=
.
