题目内容
【题目】已知四边形ABCD的对角线相交于O，给出下列 5个条件:①AB∥CD ；②AD∥BC；③AB=CD ；④∠BAD=∠BCD；⑤OA=OC．从以上5个条件中任选 2个条件为一组，能推出四边形ABCD为平行四边形的有（ ）
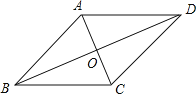
A. 4组 B. 5组 C. 6组 D. 7组
【答案】C
【解析】
有①与②，①与③，①与④，①与⑤，②与④，②与⑤，
①与②根据两组对边分别平行的四边形是平行四边形，能推出四边形ABCD为平行四边形；
①与③根据一组对边平行且相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；
①与④，②与④根据两组对角分别相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；
①与⑤，②与⑤根据对角线互相平分的四边形是平行四边形，能推出四边形ABCD为平行四边形．
所以能推出四边形ABCD为平行四边形的有6组．
故选C．
练习册系列答案
相关题目
【题目】某中学举行“校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出
名选手组成初中代表队和高中代表队参加学校决赛．每个队名选手的决赛成绩如图所示：
填表：
平均数（分） | 中位数（分） | 众数（分） | |
初中代表队 |
|
| |
高中代表队 |
|
|
结合两队决赛成绩的平均数和中位数，分析哪个代表队的成绩较好；
计算两队决赛成绩的方差，并判断哪个代表队的成绩较为稳定．
