题目内容
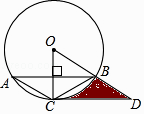
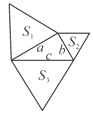
【题目】如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形。那么,这四个图形中,其面积![]() 满足
满足![]() 的个数是( )
的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】利用直角△ABC的边长就可以表示出等边三角形S1、S2、S3的大小,满足勾股定理;利用圆的面积公式表示出S1、S2、S3,然后根据勾股定理即可解答;在勾股定理的基础上结合等腰直角三角形的面积公式,运用等式的性质即可得出结论;分别用AB、BC和AC表示出 S1、S2、S3,然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系.
设直角三角形ABC的三边AB、CA、BC的长分别为a、b、c,则c2=a2+b2.
第一幅图:∵S3=![]() c2,S1=
c2,S1=![]() a2,S2=
a2,S2=![]() b2
b2
∴S1+S2=![]() (a2+b2)=
(a2+b2)=![]() c2=S3;
c2=S3;
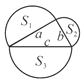
第二幅图:由圆的面积计算公式知:S3=![]() ,S2=
,S2=![]() ,S1=
,S1=![]() ,
,
则S1+S2=![]() +
+![]() =
=![]() = S3;
= S3;
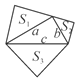
第三幅图:由等腰直角三角形的性质可得:S3=![]() c2,S2=
c2,S2=![]() b2,S1=
b2,S1=![]() a2,
a2,
则S3+S2=![]() (a2+b2)=
(a2+b2)=![]() c2=S1.
c2=S1.
第四幅图:因为三个四边形都是正方形则:
∴S3=BC2=c2,S2= AC2=b2,,S1=AB2=a2,
∴S3+S2=a2+b2=c2=S1.
故选:D.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出![]() 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队![]() 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:

![]() 填表:
填表:
平均数(分) | 中位数(分) | 众数(分) | |
初中代表队 |
|
| |
高中代表队 |
|
|
![]() 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
![]() 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.