题目内容
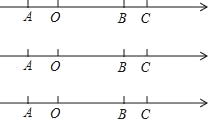
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7，满足OA=3，BC=1，P为数轴上一动点，点P从A出发，沿数轴正方向以每秒1.5个单位长度的速度匀速运动，点Q从点C出发在射线CA上向点A匀速运动，且P、Q两点同时出发．
(1)求a、b的值
(2)当P运动到线段OB的中点时，点Q运动的位置恰好是线段AB靠近点B的三等分点，求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时，求OP的长．
【答案】（1）-3,6；（2）点Q的运动速度每秒1个单位长度；（3）OP的长为0.6或6.6．
【解析】
（1）由点C表示7，可得OC=7，由OA=3，BC=1，得A、B两点表示的数，可得a、b的值；
（2）先计算P运动时间，根据点Q运动的位置恰好是线段AB靠近点B的三等分点，可知：BQ=
AB，可得点Q的路程，根据时间可得结论；
（3）设t秒时，PQ=6，分两种情况：①如图1，当Q在P的右侧时，②如图2，当Q在P的左侧时；根据PQ=6分别列式可得t的值，再计算OP的长．
（1）∵OA=3，
∴点A表示的数为﹣3，即a=﹣3，
∵C表示的数为7，
∴OC=7，
∵BC=1，
∴OB=6，
∴点B表示的数为6，即b=6；
（2）当P为OB的中点时，
AP=AO+OP=3+
OB=3+3=6，
t=
=4（s），
由题意得：BQ=AB=×（3+6）=3，
∴CQ=BQ+BC=1+3=4，
∴VQ=
=1，
答：点Q的运动速度每秒1个单位长度；
（3）设t秒时，PQ=6，
分两种情况：
①如图1，当Q在P的右侧时，
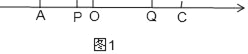
AP+PQ+CQ=3+7，
1.5t+6+t=3+7，
t=1.6，
AP=1.5t=2.4，
∴OP=3﹣2.4=0.6，
②如图2，当Q在P的左侧时，
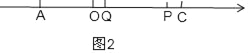
AP+CQ=AC+PQ=10+6，
1.5t+t=16，
t=6.4，
AP=1.5t=1.5×6.4=9.6，
∴OP=9.6﹣3=6.6，
综上所述，OP的长为0.6或6.6．
