题目内容
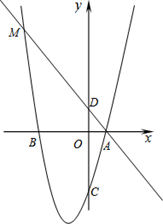
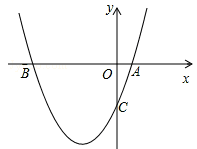
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
解:(1)∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,-4)。
∴抛物线C2的顶点坐标为(1,-4)。
∴抛物线C2的解析式为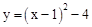 ,即
,即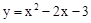 。
。
(2)证明:由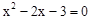 解得
解得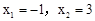 ,
,
∵点A在点B的左侧,∴A(-1,0),B(3,0),AB=4。
∵抛物线C2的对称轴为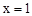 ,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
将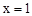 代入y=x2+3得y=4,∴E(1, 4),CE=DE。
代入y=x2+3得y=4,∴E(1, 4),CE=DE。
∴四边形ADBE是平行四边形。
∵ED⊥AB,∴四边形ADBE是菱形。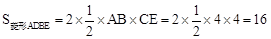 。
。
(3)存在。分AB为平行四边形的边和对角线两种情况:
①当AB为平行四边形的一边时,如图,
设F(1,y),
∵OB=3,∴G1(-2,y)或G2(4,y)。
∵点G在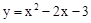 上,
上,
∴将x=-2代入,得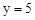 ;将x=4代入,得
;将x=4代入,得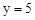 。
。
∴G1(-2,5),G2(4,5)。
②当AB为平行四边形的一对角线时,如图,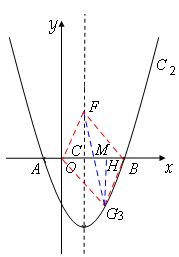
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM=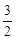 ,CM=
,CM= 。
。
∵△CFM≌△HGM(AAS),∴HM=CM= 。∴OH=2。
。∴OH=2。
∴G3(2,-y)。
∵点G在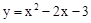 上,
上,
∴将(2,-y)代入,得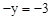 ,即
,即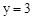 。
。
∴G3(2,-3)。
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(-2,5),G2(4,5),G3(2,-3)。
解析试题分析:(1)根据平移的性质,写出平移后的顶点坐标即可得出抛物线C2的解析式。
(2)求出点A、B、D、E的坐标,即可根据对角线互相垂直平分的四边形是菱形的判定得到证明;从而根据菱形的性质求出面积。
(3)分AB为平行四边形的边和对角线两种情况讨论即可。

如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y= (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )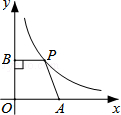
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |

 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
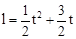 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.