题目内容
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y= (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )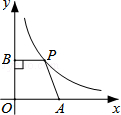
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |
C.
解析试题分析:设点P的坐标为(x, ),
),
∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,
∴四边形OAPB是个直角梯形,
∴四边形OAPB的面积= (PB+AO)×BO=
(PB+AO)×BO= (x+AO)×
(x+AO)× =
= +
+ =
= +
+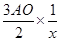 ,
,
∵AO是定值,
∴四边形OAPB的面积是个减函数,即点P的横坐标逐渐增大时四边形OAPB的面积逐渐减小.
故选C.
考点:反比例函数系数k的几何意义.

练习册系列答案
相关题目
如图,A是反比例函数 图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
| A.1 | B.2 | C.3 | D.4 |
下列函数是反比例函数的是( )
| A.y="x" | B.y=kx﹣1 | C.y= | D.y= |
如图,某反比例函数的图象过点(-2,1),则此反比例函数表达式为( )
A. | B. | C. | D. |

 ,长y宽x的函数,其函数图像大致是
,长y宽x的函数,其函数图像大致是

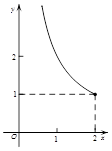 B.
B.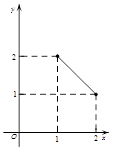 C.
C.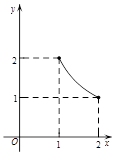 D.
D.
 上的点,A、B两点的横坐标分别是
上的点,A、B两点的横坐标分别是 、
、 ,线段AB的延长线交x轴于点C,若
,线段AB的延长线交x轴于点C,若 ,则
,则 的值为( )
的值为( )