题目内容
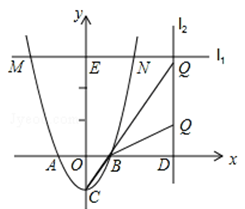
(2013年广东梅州10分)如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.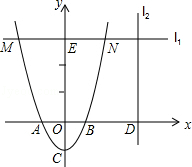
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
解:(1)∵y=2x2﹣2,∴当y=0时,2x2﹣2=0,x=±1。
∴点A的坐标为(﹣1,0),点B的坐标为(1,0),AB=2。
又当x=0时,y=﹣2,∴点C的坐标为(0,﹣2),OC=2。
∴S△ABC=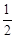 AB•OC=
AB•OC=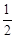 ×2×2=2。
×2×2=2。
(2)将y=6代入y=2x2﹣2,得2x2﹣2=6,x=±2,
∴点M的坐标为(﹣2,6),点N的坐标为(2,6),MN=4。
∵平行四边形的面积为8,∴MN边上的高为:8÷4=2。
∴P点纵坐标为6±2。
①当P点纵坐标为6+2=8时,2x2﹣2=8,x=±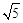 。
。
∴点P的坐标为(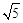 ,8)或(
,8)或(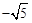 ,8)。
,8)。
②当P点纵坐标为6﹣2=4时,2x2﹣2=4,x=±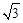 ,
,
∴点P的坐标为(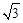 ,4)或(
,4)或(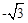 ,4)。
,4)。
综上所述,当平行四边形的面积为8时,点P的坐标为(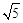 ,8)或(
,8)或(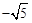 ,8)或(
,8)或(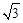 ,4)或(
,4)或(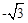 ,4)。
,4)。
(3)∵点B的坐标为(1,0),点C的坐标为(0,﹣2),∴OB=1,OC=2。
∵∠QDB=∠BOC=90°,
∴以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况:
①OB与BD边是对应边时,△OBC∽△DBQ,则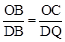 ,即
,即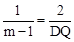 ,
,
解得DQ=2(m﹣1)=2m﹣2。
②OB与QD边是对应边时,△OBC∽△DQB,则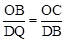 ,即
,即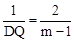 ,
,
解得 。
。
综上所述,线段QD的长为2m﹣2或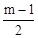 。
。
解析

 春雨教育同步作文系列答案
春雨教育同步作文系列答案如图,A是反比例函数 图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
| A.1 | B.2 | C.3 | D.4 |
 (元)与销售单价
(元)与销售单价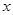 (元)之间的函数关系式;
(元)之间的函数关系式; 的图象过C点.
的图象过C点.
 .
.