题目内容
(2013年四川眉山11分)如图,在平面直角坐标系中,点A、B在x轴上,点C、D在y轴上,且OB=OC=3,OA=OD=1,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,直线AD与抛物线交于另一点M.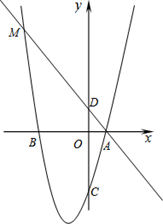
(1)求这条抛物线的解析式;
(2)P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
(3)请直接写出将该抛物线沿射线AD方向平移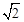 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
解:(1)根据题意得,A(1,0),D(0,1),B(﹣3,0),C(0,﹣3),
∵抛物线经过点A(1,0),B(﹣3,0),C(0,﹣3),
∴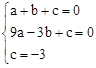 ,解得
,解得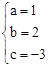 。
。
∴抛物线的解析式为:y=x2+2x﹣3。
(2)存在。△APE为等腰直角三角形,有三种可能的情形:
①以点A为直角顶点,
如图,过点A作直线AD的垂线,与抛物线交于点P,与y轴交于点F。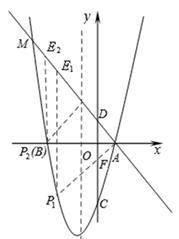
∵OA=OD=1,∴△AOD为等腰直角三角形。
∵PA⊥AD,∴△OAF为等腰直角三角形。
∴OF=1,F(0,﹣1)。
设直线PA的解析式为y=kx+b,
将点A(1,0),F(0,﹣1)的坐标代入得: ,解得
,解得 。
。
∴直线PA的解析式为y=x﹣1。
将y=x﹣1代入抛物线解析式y=x2+2x﹣3得
x2+2x﹣3=x﹣1,整理得:x2+x﹣2=0,
解得x=﹣2或x=1。
当x=﹣2时,y=x﹣1=﹣3。∴P(﹣2,﹣3)。
②以点P为直角顶点,
此时∠PAE=45°,因此点P只能在x轴上或过点A与y轴平行的直线上。
过点A与y轴平行的直线,只有点A一个交点,故此种情形不存在;
因此点P只能在x轴上,而抛物线与x轴交点只有点A、点B,故点P与点B重合,
∴P(﹣3,0)。
③以点E为直角顶点,
此时∠EAP=45°,由②可知,此时点P只能与点B重合,点E位于直线AD与对称轴的交点上。
综上所述,存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形。
点P的坐标为(﹣2,﹣3)或(﹣3,0)。
(3)y==x2+4x+1。
解析

 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推. (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.
 的图象过C点.
的图象过C点.
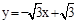 与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线
与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线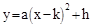 (a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和
(a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和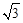 个单位长度/秒,运动时间为t秒.
个单位长度/秒,运动时间为t秒.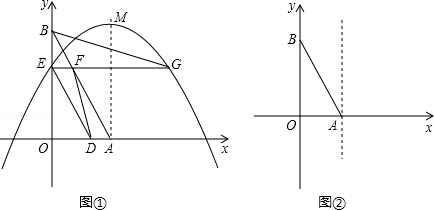
 .
.