题目内容
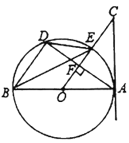
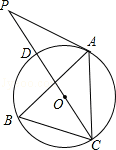
【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BAD,AC=7,AD=3![]() ,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
【答案】5![]() π
π
【解析】
连接OC、OA,作DE⊥AC于E,证明A、B、C、D四点共圆,由圆周角定理得出∠BDC=∠BAC=45°,∠DBC=∠DAC=45°,证出BC=DC,得出BD=![]() CD,证明△ADE是等腰直角三角形,得出AE=DE=
CD,证明△ADE是等腰直角三角形,得出AE=DE=![]() AD=3,求出CE=AC﹣AE=4,由勾股定理得出CD=
AD=3,求出CE=AC﹣AE=4,由勾股定理得出CD=![]() =5,则BD=5
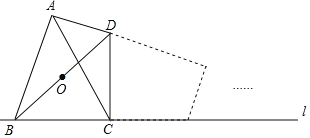
=5,则BD=5![]() ,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径为半径为OC或OA的圆的周长,即可得出答案.
,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径为半径为OC或OA的圆的周长,即可得出答案.
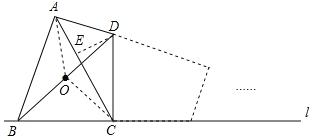
连接OC、OA,作DE⊥AC于E,如图所示:
∵∠BAD=∠BCD=90°,O为BD的中点,
∴OA=OC=![]() BD=OB=OD,A、B、C、D四点共圆,
BD=OB=OD,A、B、C、D四点共圆,
∵AC平分∠BAD,
∴∠DAC=∠BAC=45°,
∴∠BDC=∠BAC=45°,∠DBC=∠DAC=45°,
∴BC=DC,
∴BD=![]() CD,
CD,
∵DE⊥AC,
∴△ADE是等腰直角三角形,
∴AE=DE=![]() AD=3,
AD=3,
∴CE=AC﹣AE=4,
∴CD=![]()
∴BD=5![]() ,
,
将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径为半径为OC或OA的圆的周长,
∴将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度=5![]() π;
π;
故答案为:5![]() π.
π.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目