题目内容
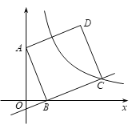
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
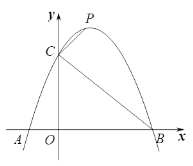
【答案】(1)5 ;(2)![]() ,
,![]() ;(3)点P坐标为(
;(3)点P坐标为(![]() ,
,![]() ).
).
【解析】
(1)分别求出点B和点C的坐标,再运用勾股定理即可求出BC的长;
(2)求出y=0和y=3时相应的x的值,结合函数的图象即可得到答案;
(3)过点P作PD⊥y轴,设点P坐标为(x, ![]() ),则点D坐标为(0,
),则点D坐标为(0, ![]() ),表示出PD,CD,证明△PDC∽△COB,得出
),表示出PD,CD,证明△PDC∽△COB,得出![]() ,列方程求解即可.
,列方程求解即可.
(1)当x=0时,y=3,
∴C(0,3),
∴OC=3
当y=0时![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
∴A(-1,0),B(4,0),
∴OA=1,OB=4
在Rt△BOC中,BC=![]() =5;
=5;
(2) 当y=0时![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
当y=3时![]() ,解得x1=0,x2=4
,解得x1=0,x2=4
∴当0≤y≤3时,![]() ,
,![]()
(3)过点P作PD⊥y轴

设点P坐标为(x, ![]() ),则点D坐标为(0,
),则点D坐标为(0, ![]() )
)
∴PD=x,CD=![]() -3=
-3=![]()
∵∠BCP=90°,
∴∠PCD+∠BCO=90°,
∵∠PCD+∠CPD=90°,
∴∠BCO=∠CPD
∵∠PDC=∠BOC=90°,
∴△PDC∽△COB
∴![]() ,
,
∴![]() ,
,
∴x=![]() 或x=0(舍去)
或x=0(舍去)
当x=![]() 时,y=
时,y=![]()
∴点P坐标为(![]() ,
,![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】某公司到果园基地购买某种水果慰问医务工作者,果园基地向购买超过![]() 以上(含
以上(含![]() )的客户推出两种购买方式.方式甲:价格为
)的客户推出两种购买方式.方式甲:价格为![]() 元
元![]() ,由果园基地运送到公司;方式乙:价格为
,由果园基地运送到公司;方式乙:价格为![]() 元
元![]() ,由顾客自己租车运回,从果园基地到公司的租车费用为
,由顾客自己租车运回,从果园基地到公司的租车费用为![]() 元.设该公司购买水果的数量为
元.设该公司购买水果的数量为![]() (
(![]() ).
).
(1)根据题意,填写下表:
购买水果的数量(kg) |
|
|
| … |
方式甲的总费用(元) |
| … | ||
方式乙的总费用(元) |
| … |
(2)设该公司按方式甲购买水果的总费用为![]() 元,按方式乙购买水果的总费用为
元,按方式乙购买水果的总费用为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若按方式甲购买水果的总费用和按方式乙购买水果的总费用相同,则该公司购买水果的数量为 ![]() ;
;
② 若该公司购买水果的数量为![]() ,则按方式甲、方式乙中的方式 购买水果的总费用少;
,则按方式甲、方式乙中的方式 购买水果的总费用少;
③ 若该公司购买水果的总费用为![]() 元,则按方式甲、方式乙中的方式 购买水果的数量多.
元,则按方式甲、方式乙中的方式 购买水果的数量多.
【题目】今年是脱贫攻坚决胜之年,我市某乡为了增加农民收入,决定利用当地优质山林土地资源发展园林绿化树苗培育产业.前期由乡农技站引进“银杏”、“罗汉松”、“广玉兰”、“竹柏”四个品种共![]() 棵幼苗进行试育成苗实验,并把实验数据绘制成下图所示的扇形统计图和不完整的条形统计图,已知实验中竹柏的成苗率是
棵幼苗进行试育成苗实验,并把实验数据绘制成下图所示的扇形统计图和不完整的条形统计图,已知实验中竹柏的成苗率是![]() .
.
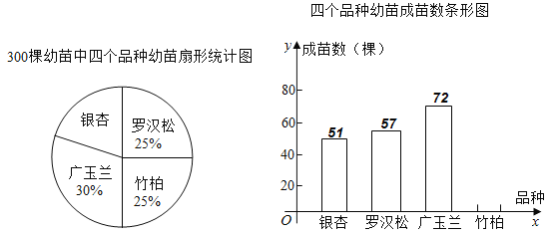
(1)请你补全条形统计图;
(2)如果从这![]() 棵实验幼苗中随机抽取一棵幼苗,求它能成苗的概率;
棵实验幼苗中随机抽取一棵幼苗,求它能成苗的概率;
(3)根据市场调查,这四个品种的树苗的幼苗进价、成苗售价和市场需求如下表所示:
树苗品种 | 银杏 | 罗汉松 | 广玉兰 | 竹柏 |
每棵幼苗进价(元) |
|
|
|
|
每棵成苗售价(元) |
|
|
|
|
市场需求(万棵) |
|
|
|
|
假设除了购买幼苗外,培育每棵成苗还需肥料等支出![]() 元(未成功培育成成苗的此项支出忽略不计),该乡根据市场需求组织
元(未成功培育成成苗的此项支出忽略不计),该乡根据市场需求组织![]() 村农民培育银杏树苗和罗汉松树苗并将全部成苗销售完成后,可为本乡
村农民培育银杏树苗和罗汉松树苗并将全部成苗销售完成后,可为本乡![]() 村农民增加收入多少万元?
村农民增加收入多少万元?