题目内容
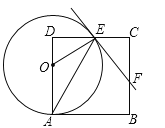
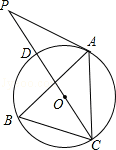
【题目】如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
【答案】(1)证明:连接OA。
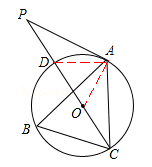
∵∠B=60°,∴∠AOC=2∠B=120°。
又∵OA=OC,∴∠ACP=∠CAO=30°。∴∠AOP=60°。
∵AP=AC,∴∠P=∠ACP=30°。∴∠OAP=90°。∴OA⊥AP。
∴AP是⊙O的切线。
(2)解:连接AD。
∵CD是⊙O的直径,∴∠CAD=90°。∴AD=ACtan30°=3×![]() 。
。
∵∠ADC=∠B=60°,∴∠PAD=∠ADC﹣∠P=60°﹣30°。
∴∠P=∠PAD。∴PD=AD=![]() 。
。
【解析】(1)连接OA,由∠B=60°,利用圆周角定理,即可求得∠AOC的度数,又由OA=OC,即可求得∠OAC与∠OCA的度数,利用三角形外角的性质,求得∠AOP的度数,又由AP=AC,利用等边对等角,求得∠P,则可求得∠PAO=90°,则可证得AP是⊙O的切线。
(2)由CD是⊙O的直径,即可得∠DAC=90°,然后利用三角函数与等腰三角形的判定定理,即可求得PD的长。

练习册系列答案
相关题目
【题目】某天,一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
(1)该经营户所批发的西红柿和豆角的质量分别为多少 kg?
(2)如果西红柿和豆角全部以零售价售出,他当天卖出这些西红柿和豆角赚了多少钱?