题目内容
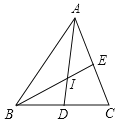
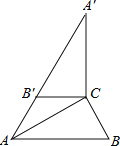
【题目】如图，在△ABC中，∠ACB＝90°，∠B＝60°，BC＝2．将△ABC绕点C顺时针旋转，得到△A′B′C，连接AB′，且A，B′，A′在同一条直线上，则AA′＝_____．
【答案】6．
【解析】
根据直角三角形中边角关系得出AB＝4，∠BAC＝30°，根据旋转的性质，对应角相等，对应边相等，得到A′B′＝AB＝4，∠A′＝∠BAC＝30°，∠A′B′C＝∠B＝60°，AC＝A′C．由等腰三角形的性质得到∠CAB′＝∠A′＝30°，再由邻补角的定义计算出∠AB′C的度数，最后由三角形内角和性质得到相等角，判断出AB′＝B′C＝BC＝2．即可解决.
由在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，得
AB＝4，∠BAC＝30°．
由旋转的性质，得
A′B′＝AB＝4，∠A′＝∠BAC＝30°，∠A′B′C＝∠B＝60°，AC＝A′C．
由等腰三角形的性质，得
∠CAB′＝∠A′＝30°．
由邻补角的定义，得
∠AB′C＝180°﹣∠A′B′C＝120°．
由三角形的内角和定理，得
∠ACB′＝180°﹣∠AB′C﹣∠B′AC＝30°．
∴∠B′AC＝∠B′CA＝30°，
AB′＝B′C＝BC＝2．
A′A＝A′B′+AB′＝4+2＝6，
故答案为：6．
练习册系列答案
相关题目
【题目】小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第
天的销售量与销售单价如下（每天内单价和销售量保持一致）：
销售量 |
|
销售单价 | 当 |
当 |
设第天的利润
元．
（1）请计算第几天该品种草莓的销售单价为25元/千克？
（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润＝（售价－成本）×销售量
