题目内容
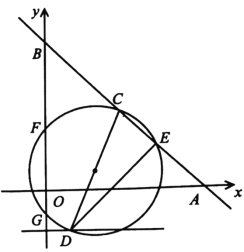
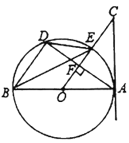
【题目】如图，
是
的直径，
是的切线，连接
交于E，过点A作
于F，交于D，连接
，
．
（1）求证：
；
（2）若
，
，求
的长．
【答案】（1）见解析；（2）
.
【解析】
（1）根据切线的性质可得∠CAF+∠BAD=90°，根据同角的余角相等可得
，进一步根据圆周角定理的推论即可证得结论；
（2）由（1）的结论和正切的定义在直角△OAC中可求得AC的长，再在直角△ACF中利用正切的定义和勾股定理即可求出结果.
解：（1）证明：∵
是
的切线，∴∠CAO=90°，即∠CAF+∠BAD=90°，
∵
，∴∠AFC=90°，∴∠CAF+∠C=90°，
∴，
∵
，
∴
；
（2）∵
是的直径，
，∴AO=6，
∵，
，
∴
，∴AC=8，
在直角△ACF中，∵
，∴设AF=3x，CF=4x，则由勾股定理得：AC=5x，
∴5x=8，∴
，∴
.
练习册系列答案
相关题目
【题目】小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第
天的销售量与销售单价如下（每天内单价和销售量保持一致）：
销售量 |
|
销售单价 | 当 |
当 |
设第天的利润
元．
（1）请计算第几天该品种草莓的销售单价为25元/千克？
（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润＝（售价－成本）×销售量
