Question

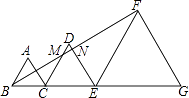
【题目】如图，△ABC、△DCE、△FEG为等边三角形，边长分别为2、3、5，且从左至右如图排列，连接BF，交DC、DE分别于M、N两点，则△DMN的面积为 ．

Answer 1

【答案】
【解析】解：∵△FEG为等边三角形，∴∠FEG=60°． ∵BC=2，CE=3，EF=5，∴BE=5=EF，
∴∠EBF=∠EFB= ∠FEG=30°．
∵△DCE为等边三角形，
∴∠D=∠DCE=∠DEC=60°，
∴∠DNM=∠EBF+∠DEC=90°．
∵∠DCE=∠FEG=60°，
∴CM∥EF，
∴△BCM∽△BEF，
∴ = ，即 = ，
解得CM=2，
∴DM=DC﹣CM=3﹣2=1，
∴在Rt△DNM中，
MN=DMsin60°= ，
DN=DMcos60°= ，
∴S△DNM= DNMN= ．
故答案为 ．

易证BE=EF=5，从而可得∠EBF= ∠FEG=30°，根据三角形外角的性质可得到∠DNM=90°；易证△BCM∽△BEF，根据相似三角形的性质可求出CM，从而得到DM的值，然后在Rt△DNM中，运用三角函数可求出MN、DN，就可求出△DMN的面积．