题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b2=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论是 ． （写出正确命题的序号）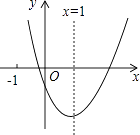 
【答案】①④
【解析】解：由二次函数图象开口向上，得到a＞0；与y轴交于负半轴，得到c＜0， ∵对称轴在y轴右侧，且﹣ 
=1，即2a+b=0，
∴a与b异号，即b＜0，
∴abc＞0，选项①正确；
∵二次函数图象与x轴有两个交点，
∴△=b2﹣4ac＞0，即b2＞4ac，选项②错误；
∵原点O与对称轴的对应点为（2，0），
∴x=2时，y＜0，即4a+2b+c＜0，选项③错误；
∵x=﹣1时，y＞0，
∴a﹣b+c＞0，
把b=﹣2a代入得：3a+c＞0，选项④正确，
故答案是：①④．
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本，需要知道二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
期末集结号系列答案
【题目】某鲜花销售部在春节前20天内销售一批鲜花．其中，该销售部公司的鲜花批发部日销售量y1（万朵）与时间x（x为整数，单位：天）关系为二次函数，部分对应值如表所示．
时间x（天） | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1（万朵） | 0 | 16 | 24 | 24 | 16 | 0 |
与此同时，该销售部还通过某网络电子商务平台销售鲜花，网上销售日销售量y2（万朵）与时间x（x为整数，单位：天） 的函数关系如图所示．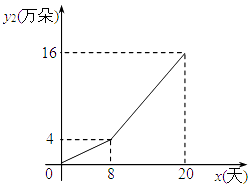
（1）求y1与x的二次函数关系式及自变量x的取值范围；
（2）求y2与x的函数关系式及自变量x的取值范围；
（3）当8≤x≤20时，设该花木公司鲜花日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时的最大值．
