Question

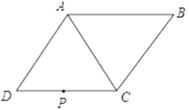
【题目】如图，在菱形ABCD中，∠ADC＝60°，CD＝4cm，P为CD的中点．

（1）在AC上找一点Q，使DQ+PQ的值最小（保留画图痕迹，不写画法，不必说理）；

（2）求出（1）中DQ+PQ的长．

Answer 1

【答案】（1）见解析；（2）2cm

【解析】

（1）如图，连接 PB 交 AC 于点 Q，点 Q 是所求作的；

（2）连接 PA．证明△PAB 是直角三角形，利用勾股定理求出 PB 即可；

解：（1）如图，连接 PB 交 AC 于点 Q，点 Q 是所求作的；

（2）连结 AP，

在菱形 ABCD 中，AB＝AD＝CD＝4cm，又∵∠ADC＝60°，

∴△ACD 为等边三角形，

∵P 为 CD 的中点，

AP⊥CD，DP＝ CD＝2 cm， 在 Rt△ADP 中，

∴AP＝＝6（cm），

∵AP⊥CD，AB∥CD，

∴AP⊥AB，

在 Rt△ABP 中，BP＝＝（cm），

在菱形 ABCD 中，AC⊥BD，OB＝OD

∴DQ＝BQ

∴DQ+PQ＝BQ+PQ＝BP＝2（cm）．

答：DQ+PQ 的长为 2cm．