题目内容
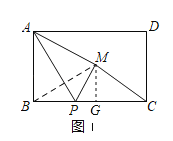
【题目】如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为_____.

【答案】![]() 或
或![]() 或8
或8
【解析】
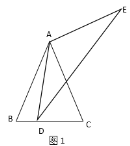
分三种情况:①BM=CM时,如图1所示:作MG⊥BC于G,则BG=CG=![]() BC=4,∠BGM=90
BC=4,∠BGM=90![]() ,设BP=x,由折叠的性质和相似三角形的性质得到MG,由勾股定理得出方程,解方程即可;②BM=BC=8时,如图2所示:根据折叠的性质得到BO=MO,根据相似三角形的性质健康得到结论;③CM=BC时,连接OC,如图3,由折叠的性质即可得到结论.
,设BP=x,由折叠的性质和相似三角形的性质得到MG,由勾股定理得出方程,解方程即可;②BM=BC=8时,如图2所示:根据折叠的性质得到BO=MO,根据相似三角形的性质健康得到结论;③CM=BC时,连接OC,如图3,由折叠的性质即可得到结论.
解:当△BMC为等腰三角形时,分三种情况:
①BM=CM时,如图1所示:
作MG⊥BC于G,则BG=CG=![]() BC=4,∠BGM=90°,
BC=4,∠BGM=90°,
设BP=x,
由折叠的性质得:MP=BP=x,AP垂直平分BM,
∵∠ABC=90°,
∴∠MBG=∠BAP,
∴△BGM∽△ABP,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:MG=![]() x,
x,
在Rt△PMG中,GP=4﹣x,由勾股定理得:(4﹣x)2+(![]() x)2=x2,
x)2=x2,
解得:x=![]() ,或x=10(不合题意舍去),
,或x=10(不合题意舍去),
∴BE=![]() ;
;
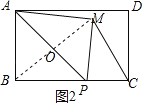
②BM=BC=8时,如图2所示:
由折叠的性质得:BO=MO=![]() BM=4,AP⊥BP,
BM=4,AP⊥BP,
∴∠AOB=∠ABP=90°,
∵∠BAO=∠BAP,
∴△ABP∽△AOB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:BP=![]() ;
;
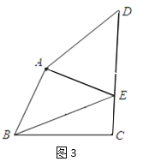
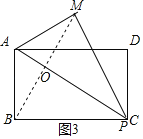
③CM=BC时,连接OC,如图3所示:
由折叠的性质得:AP垂直平分BM,
∵CM=BC,
∴OC⊥BM,
∴点P与C重合,
∴BP=BC=8;
综上所述,当△BMC为等腰三角形时,BP的长为![]() 或
或![]() 或8;
或8;
故答案为:![]() 或
或![]() 或8.
或8.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
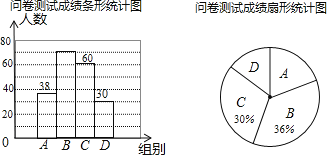
小学生10分钟应用题系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.