题目内容
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
【答案】(1)600元;(2)单价定为29元,每月获得最大利润4410元;(3)500元
【解析】
(1)把x=20代入y=10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由总利润=销售量每件纯赚利润,得w=(x8)(10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令10x2+580x4000=3410,求出x的值,结合图象求出利润的范围,然后设政府每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
解:(1)当x=20时,y=10x+500=10×20+500=300,
300×(108)=300×2=600元,
即政府这个月为他承担的总差价为600元.
(2)由题意得,w=(x8)(10x+500)=10x2+580x4000=-10(x-29)2+4410,
∵a=10<0,
∴当x=29时,w有最大值4410元.
即当销售单价定为29元时,每月可获得最大利润4410元.
(3)由题意得:10x2+580x4000=3410,
解得:x1=19,x2=39.
∵a=10<0,抛物线开口向下,
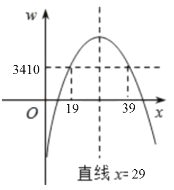
∴结合图象可知:当19≤x≤39时,w≥3410.
又∵x≤25,
∴当19≤x≤25时,w≥3410.
设政府每个月为他承担的总差价为p元,
∴p=(108)×(10x+500)
=20x+1000.
∵20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
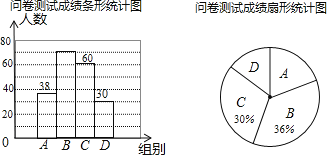
仁爱英语同步练习册系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.