题目内容
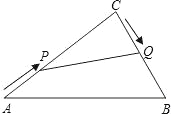
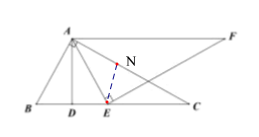
【题目】如图,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,且
重合)点,且![]() 于
于![]() 相交于点
相交于点![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)当![]() 时,证明:
时,证明:![]() .
.
(3)![]() 面积的最小值是_______.
面积的最小值是_______.
(4)当![]() 的内心在
的内心在![]() 的外部时,直接写出
的外部时,直接写出![]() 的范围______.
的范围______.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据锐角三角函数的定义以及三角形内角和定理,即可求解;
(2)由ASA,即可证明![]() ;
;
(3)由题意得:![]() 面积=
面积=![]() AE2,当AE⊥BC时,AE=
AE2,当AE⊥BC时,AE=![]() ,进而即可求解;
,进而即可求解;
(4)当![]() 的内心恰好落在AC上时,设
的内心恰好落在AC上时,设![]() 的内心为N,易证
的内心为N,易证![]() 是等边三角形,此时,AE=2,进而即可得到结论.
是等边三角形,此时,AE=2,进而即可得到结论.
(1)∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 180°-90°-60°=30°.
180°-90°-60°=30°.
故答案是:![]() ;
;
(2)![]() 于
于![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ;
;
(3)∵![]() =60°,
=60°,
∴EF=![]() AE,
AE,
∴![]() 面积=
面积= ![]() EFAE=
EFAE=![]() AE2,
AE2,
∴当AE的长最小时,![]() 面积的最小,即:AE⊥BC时,
面积的最小,即:AE⊥BC时,![]() 面积的最小.
面积的最小.
∴AE的最小值=ABsin60°=2×![]() =
=![]() ,此时,
,此时,![]() 面积的最小值=
面积的最小值=![]() .
.
故答案是:![]() .
.
(4)当![]() 的内心恰好落在AC上时,设
的内心恰好落在AC上时,设![]() 的内心为N,连接EN,
的内心为N,连接EN,
∵N是![]() 的内心,
的内心,
∴AN平分∠EAF,EN平分∠AEF,
∴∠EAC=![]() ∠EAF=30°,
∠EAF=30°,
∵∠BAC=90°,
∴∠BAE=∠BAC-∠EAC=90°-30°=60°,
又∵∠B=60°,
∴![]() 是等边三角形,
是等边三角形,
∴AE=AB=2,
∵![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,由(1)可知
重合)点,由(1)可知![]() ,
,
∴当![]() 的内心在
的内心在![]() 的外部时,
的外部时,![]() .
.
故答案是:![]() .
.

 名题金卷系列答案
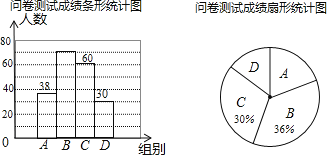
名题金卷系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.