Question

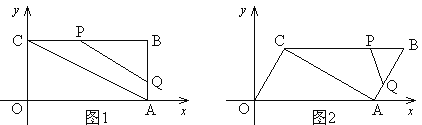
【题目】如图，平面直角坐标系中，一次函数y＝x﹣1的图象与x轴，y轴分别交于点A，B，与反比例函数y＝的图象交于点C，D，CE⊥x轴于点E，．

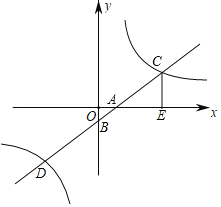
（1）求反比例函数的表达式与点D的坐标；

（2）以CE为边作ECMN，点M在一次函数y＝x﹣1的图象上，设点M的横坐标为a，当边MN与反比例函数y＝的图象有公共点时，求a的取值范围．

Answer 1

【答案】（1）D（﹣3，﹣4）；（2）当边MN与反比例函数y＝的图象有公共点时4＜a≤6或﹣3＜a≤﹣2．

【解析】

（1）利用待定系数法以及等腰直角三角形的性质求出EC，OE即可解决问题．

（2）如图，设M（a，a﹣1），则N（a，），由EC＝MN构建方程求出特殊点M的坐标即可判断．

解：（1）由题意A（1，0），B（0，﹣1），

∴OA＝OB＝1，

∴∠OAB＝∠CAE＝45°

∵AE＝3OA，

∴AE＝3，

∵EC⊥x轴，

∴∠AEC＝90°，

∴∠EAC＝∠ACE＝45°，

∴EC＝AE＝3，

∴C（4，3），

∵反比例函数y＝经过点C（4，3），

∴k＝12，

由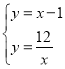，解得或，

∴D（﹣3，﹣4）．

（2）如图，设M（a，a﹣1），则N（a，）

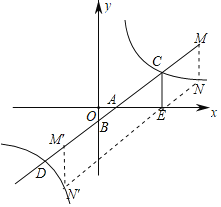
∵四边形ECMN是平行四边形，

∴MN＝EC＝3，

∴|a﹣1﹣|＝3，

解得a＝6或﹣2或﹣1±（舍弃），

∴M（6，5）或（﹣2，﹣3），

观察图象可知：当边MN与反比例函数y＝的图象有公共点时4＜a≤6或﹣3＜a≤﹣2．