Question

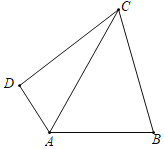
【题目】如图，在四边形ABCD中，∠DAB＝120°，∠DCB＝60°，CB＝CD，AC＝8，则四边形ABCD的面积为__．

Answer 1

【答案】16

【解析】

延长AB至点E，使BE＝DA，连接CE，作CF⊥AB于F，证明△CDA≌△CBE，根据全等三角形的性质得到CA＝CE，∠BCE＝∠DCA，得到△CAE为等边三角形，根据等边三角形的性质计算，得到答案．

延长AB至点E，使BE＝DA，连接CE，作CF⊥AB于F，

∵∠DAB+∠DCB＝120°+60°＝180°，

∴∠CDA+∠CBA＝180°，又∠CBE+∠CBA＝180°，

∴∠CDA＝∠CBE，

在△CDA和△CBE中，

，

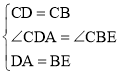∴△CDA≌△CBE（SAS）

∴CA＝CE，∠BCE＝∠DCA，

∵∠DCB＝60°，

∴∠ACE＝60°，

∴△CAE为等边三角形，

∴AE＝AC＝8，CF＝AC＝4，

则四边形ABCD的面积＝△CAB的面积＝×8×4＝16，

故答案为：16．