题目内容
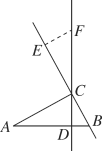
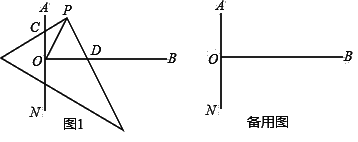
【题目】如图1,射线OB与直线AN垂直于点O,线段OP在∠AOB内,一块三角板的直角顶点与点P重合,两条直角边分别与AN、OB的交于点C、D.
(1)当∠POB=60°,∠OPC=30°,PC=2时,则PD= .
(2)若∠POB=45°,
①当PC与PO重合时,PC和PD之间的数量关系是 ;
②当PC与PO不重合时,猜想PC与PD之间的数量关系,并证明你的结论.
【答案】(1)2![]() (2)①PC=PD;②PC=PD
(2)①PC=PD;②PC=PD
【解析】(1)、作PE⊥AN于E,根据Rt△ECP的性质得出EP的长度,然后根据Rt△OPE的性质求出OP的长度,最后根据等边三角形的性质得出答案;(2)、根据题意得出△PCD为等腰直角三角形,从而得出答案;作PE⊥AN于E,PF⊥OB于F,根据矩形的性质以及角平分线的性质得出△EPC和△FPD全等,从而得出答案.
(1)、作PE⊥AN于E,∵∠POB=60°,OB⊥AN,∴∠AOP=30°,又∠OPC=30°,
∴∠ECP=60°,∴EP=PCsin∠ECP=![]() ,∴OP=2EP=2
,∴OP=2EP=2![]() ,∵∠POB=60°,∠OPD=60°,
,∵∠POB=60°,∠OPD=60°,
∴△POD是等边三角形,∴PD=PO=2![]() ;
;
(2)、①当∠POB=45°时,∵三角板的直角顶点与点P重合,
∴PC与PO重合时,△PCD为等腰直角三角形, ∴PC=PD,
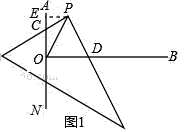
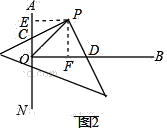
②PC=PD,理由如下:作PE⊥AN于E,PF⊥OB于F,∵AN⊥OB,PE⊥AN,PF⊥OB,
∴四边形EOFP为矩形,∴∠EPF=90°,∴∠EPC=∠FPD,∵∠POB=45°,∴∠POA=45°,
∴OP平分∠EOF,又PE⊥AN,PF⊥OB,∴PE=PF,
在△EPC和△FPD中,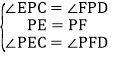 , ∴△EPC≌△FPD, ∴PC=PD.
, ∴△EPC≌△FPD, ∴PC=PD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目