题目内容
【题目】己知有理数![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() 三点,且
三点,且![]() 满足:①多项式
满足:①多项式![]() 是关于
是关于![]() 的二次三项式:②
的二次三项式:②![]()
![]() 请在图1的数轴上描出
请在图1的数轴上描出![]() 三点,并直接写出
三点,并直接写出![]() 三数之间的大小关系(用“<”连接) ;
三数之间的大小关系(用“<”连接) ;
![]() 点
点![]() 为数轴上
为数轴上![]() 点右侧一点,且点
点右侧一点,且点![]() 到
到![]() 点的距离是到
点的距离是到![]() 点距离的
点距离的![]() 倍,求点
倍,求点![]() 在数轴上所对应的有理数;
在数轴上所对应的有理数;
![]() 点
点![]() 在数轴上以每秒
在数轴上以每秒![]() 个单位长度的速度向左运动,同时点
个单位长度的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动(其中
个单位长度的速度向右运动(其中![]() ),若在整个运动的过程中,点
),若在整个运动的过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求
的距离差始终不变,求![]() 的值.
的值.
【答案】(1)a<b<c;(2)点P在数轴上所对应的有理数是12;(3)m=![]() .
.
【解析】
(1)根据题意列方程即可得到结论;
(2)设点P在数轴上所对应的有理数为x,列方程即可得到结论;
(3)设运动时间为t,根据题意列方程即可得到结论.
解:(1)∵多项式![]() 是关于
是关于![]() 的二次三项式,
的二次三项式,
∴![]() =2,a-2≠0,
=2,a-2≠0,
∴a=﹣2,
∵(b-1)2+![]() =0,
=0,
∴b-1=0,c-5=0,
∴b=1,c=5,
∴a,b,c三数之间的大小关系为a<b<c,
如图,在图1数轴上描出A、B、C三点位置.
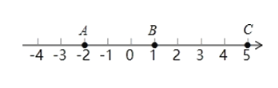
故答案为:a<b<c.
(2)设点P在数轴上所对应的有理数为x,
由题意得,x+2=2(x-5),
解得:x=12,
∴点P在数轴上所对应的有理数是12;
(3)设运动时间为t,此时A对应的数为(-2-t);B对应的数为(1+mt);C对应的数为(5+4t).
根据题意得,[(1+mt)-(-2-t)]-[(5+4t)-(1+mt)]=[1-(-2)]-(5-1),
解得:m=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目