题目内容
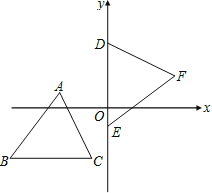
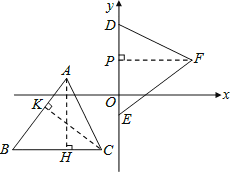
【题目】如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点在方程式y=-3的图形上,D、E两点在y轴上,则F点到y轴的距离为何?( )
A. 2B. 3C. 4D. 5
【答案】C
【解析】
试题如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P.由AB=BC,△ABC≌△DEF,就可以得出△AKC≌△CHA≌△DPF,就可以得出结论.
试题解析:如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P.
∴∠DPF=∠AKC=∠CHA=90°.
∵AB=BC,
∴∠BAC=∠BCA.
在△AKC和△CHA中
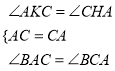 ,
,
∴△AKC≌△CHA(ASA),
∴KC=HA.
∵B、C两点在方程式y=-3的图形上,且A点的坐标为(-3,1),
∴AH=4.
∴KC=4.
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF.
在△AKC和△DPF中,
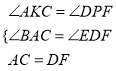 ,
,
∴△AKC≌△DPF(AAS),
∴KC=PF=4.
故选C.

练习册系列答案
相关题目