Question

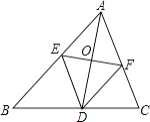
【题目】如图，Rt△ABC中，∠C=90°，AC=，tanB=，半径为2的⊙C，分别交AC，BC于点D，E，得到 ．

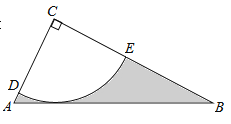
（1）求证：AB为⊙C的切线；
（2）求图中阴影部分的面积．

Answer 1

【答案】
（1）

证明：过点C作CH⊥AB于H，如图，

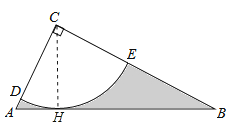
在Rt△ABC中，∵tanB==，

∴BC=2AC=，

∴AB===5，

∵CHAB=ACBC，

∴CH==2，

∵⊙C的半径为2，

∴CH为⊙C的半径，

而CH⊥AB，

∴AB为⊙C的切线；

（2）

解：S阴影部分=S△ACB﹣S扇形CDE

=×2×5﹣

=5﹣π．

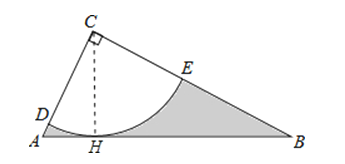
【解析】（1）过点C作CH⊥AB于H，如图，先在Rt△ABC中，利用正切的定义计算出BC=2AC=2，再利用勾股定理计算出AB=5，接着利用面积法计算出CH=2，则可判断CH为⊙C的半径，然后根据切线的判定定理即可得到AB为⊙C的切线；
（2）根据三角形面积公式和扇形的面积公式，利用S阴影部分=S△ACB﹣S扇形CDE进行计算即可．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对切线的判定定理的理解，了解切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．