ЬтФПФкШн
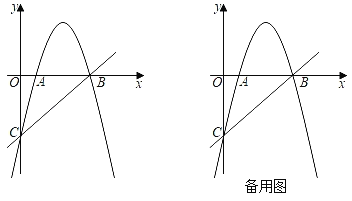
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=xЃЋ4гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌХзЮяЯпy=Ѓx2ЃЋbxЃЋcОЙ§AЁЂBСНЕуЃЌВЂгыxжсНЛгкСэвЛЕуCЃЈЕуCЕуAЕФгвВрЃЉЃЌЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЎ
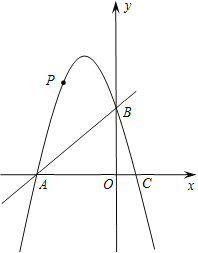
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
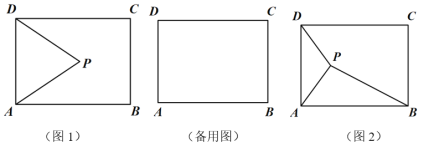
ЃЈ2ЃЉШєЕуPдкЕкЖўЯѓЯоФкЃЌЙ§ЕуPзїPDЁЭжсгкDЃЌНЛABгкЕуEЃЎЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЯпЖЮPEзюГЄЃПДЫЪБPEЕШгкЖрЩйЃП
ЃЈ3ЃЉШчЙћЦНаагкxжсЕФЖЏжБЯпlгыХзЮяЯпНЛгкЕуQЃЌгыжБЯпABНЛгкЕуNЃЌЕуMЮЊOAЕФжаЕуЃЌФЧУДЪЧЗёДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїMONЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Ѓx2Ѓ3xЃЋ4ЃЌCЃЈ1ЃЌ0ЃЉЃЈ2ЃЉЕБt=-2ЪБЃЌЯпЖЮPEЕФГЄЖШгазюДѓжЕ4ЃЌДЫЪБPЃЈЃ2ЃЌ6ЃЉЃЈ3ЃЉДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїMONЮЊЕШбќШ§НЧаЮЃЎЫљЧѓQЕуЕФзјБъЮЊ
ЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉ
ЃЌ2ЃЉ
ЁОНтЮіЁП
НтЃКЃЈ1ЃЉЁпжБЯпy=x+4гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЁрAЃЈЃ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЎ
ЁпХзЮяЯпy=Ѓx2ЃЋbxЃЋcОЙ§AЁЂBСНЕуЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрХзЮяЯпНтЮіЪНЮЊy=Ѓx2Ѓ3xЃЋ4ЃЎ
Сюy=0ЃЌЕУЃx2Ѓ3xЃЋ4=0ЃЌНтЕУx1=Ѓ4ЃЌx2=1ЃЌ
ЁрCЃЈ1ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌ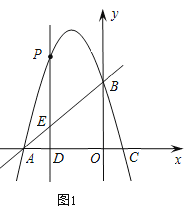
ЩшDЃЈtЃЌ0ЃЉЃЎ
ЁпOA=OBЃЌЁрЁЯBAO=45ЁуЃЎ
ЁрEЃЈtЃЌtЃЋ4ЃЉЃЌPЃЈtЃЌЃt2Ѓ3tЃЋ4ЃЉЃЎ
PE=yPЃyE=Ѓt2Ѓ3tЃЋ4ЃtЃ4=Ѓt2Ѓ4t=ЃЃЈt+2ЃЉ2+4ЃЎ
ЁрЕБt=-2ЪБЃЌЯпЖЮPEЕФГЄЖШгазюДѓжЕ4ЃЌДЫЪБPЃЈЃ2ЃЌ6ЃЉЃЎ
ЃЈ3ЃЉДцдкЃЎШчЭМ2ЃЌЙ§NЕузїNHЁЭxжсгкЕуHЃЎ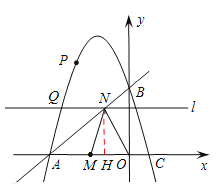
ЩшOH=mЃЈmЃО0ЃЉЃЌЁпOA=OBЃЌЁрЁЯBAO=45ЁуЃЎ
ЁрNH=AH=4ЃmЃЌЁрyQ=4ЃmЃЎ
гжMЮЊOAжаЕуЃЌЁрMH=2ЃmЃЎ
ЕБЁїMONЮЊЕШбќШ§НЧаЮЪБЃК
ЂйШєMN=ONЃЌдђHЮЊЕзБпOMЕФжаЕуЃЌ
Ёрm=1ЃЌЁрyQ=4Ѓm=3ЃЎ
гЩЃxQ2Ѓ3xQЃЋ4=3ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрЕуQзјБъЮЊЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
ЂкШєMN=OM=2ЃЌдђдкRtЁїMNHжаЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКMN2=NH2ЃЋMH2ЃЌМД22=ЃЈ4ЃmЃЉ2ЃЋЃЈ2ЃmЃЉ2ЃЌ
ЛЏМђЕУm2Ѓ6mЃЋ8=0ЃЌНтЕУЃКm1=2ЃЌm2=4ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЁрyQ=2ЃЌгЩЃxQ2Ѓ3xQЃЋ4=2ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрЕуQзјБъЮЊЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЂлШєON=OM=2ЃЌдђдкRtЁїNOHжаЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКON2=NH2ЃЋOH2ЃЌМД22=ЃЈ4ЃmЃЉ2ЃЋm2ЃЌ
ЛЏМђЕУm2Ѓ4mЃЋ6=0ЃЌЁпЁї=Ѓ8ЃМ0ЃЌ
ЁрДЫЪБВЛДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїMONЮЊЕШбќШ§НЧаЮЃЎ
злЩЯЫљЪіЃЌДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїMONЮЊЕШбќШ§НЧаЮЃЎЫљЧѓQЕуЕФзјБъЮЊ
ЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ3ЃЉЛђЃЈ
ЃЌ3ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЪзЯШЧѓЕУAЁЂBЕуЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂЧѓГіХзЮяЯпгыxжсСэвЛНЛЕуCЕФзјБъЃЎ
ЃЈ2ЃЉЧѓГіЯпЖЮPEГЄЖШЕФБэДяЪНЃЌЩшDЕуКсзјБъЮЊtЃЌдђПЩвдНЋPEБэЪОЮЊЙигкtЕФЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЧѓМЋжЕЕФЗНЗЈЧѓГіPEГЄЖШЕФзюДѓжЕЃЎ
ЃЈ3ЃЉИљОнЕШбќШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэЃЌНЋжБЯпlЕФДцдкадЮЪЬтзЊЛЏЮЊвЛдЊЖўДЮЗНГЬЮЪЬтЃЌЭЈЙ§вЛдЊЖўДЮЗНГЬЕФХаБ№ЪНПЩжЊжБЯпlЪЧЗёДцдкЃЌВЂЧѓГіЯргІQЕуЕФзјБъЃЎ ЁАЁїMONЪЧЕШбќШ§НЧаЮЁБЃЌЦфжаАќКЌШ§жжЧщПіЃКMN=ONЃЌMN=OMЃЌON=OMЃЌж№вЛЬжТлЧѓНтЃЎ