Question

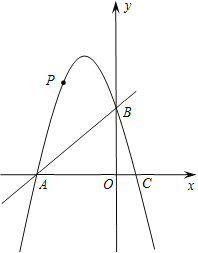
【题目】如图，在四边形中，，．

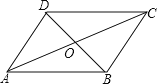
（1）求证：四边形为平行四边形；

（2）若，，求四边形的面积．

Answer 1

【答案】（1）见解析；（2）120

【解析】

（1）由可得两对内错角，，再加上已知，可用AAS证明，所以，进而可用“一组对边平行且相等的四边形是平行四边形”的判定定理即可证为平行四边形；

（2）在中，可得,至此，用勾股定理的逆定理可判断定△AOD为直角三角形，然后再利用平行四边形面积公式进行求解即可．

证明：（1）∵，

∴，，

∵，

∴，

∴，

又∵AB//CD，

∴四边形为平行四边形；

（2）∵ 四边形ABCD为平行四边形，

∴,

又∵AD=12，OD=OB=5，

∴OD 2 + AD 2 =52+122=169， OA 2 = 132=169，BD=10，

∴OD2+AD2=OA2，

∴∠ADB=90°，

∴S四边形ABCD=ADBD=12×10=120．