题目内容
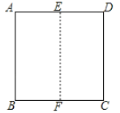
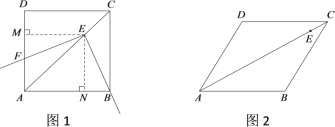
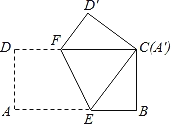
【题目】如图，将长为8cm，宽4cm的矩形纸片ABCD折叠，使点A与C重合，则折痕EF的长为（ ）
A.8cmB.4
cmC.5cmD.2
cm
【答案】D
【解析】
如图，首先证明四边形AECF为菱形，运用勾股定理分别求出CE，AC的长度，运用菱形的面积公式，即可解决问题．
解：如图，连接AF，AC，
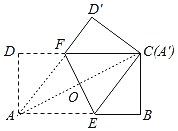
∵将长为8cm，宽4cm的矩形纸片ABCD折叠，
∴EF⊥AC，OA＝OC，AE＝CE，AF＝CF，
∵四边形ABCD为矩形，
∴FC∥AE，∠OAE＝∠OCF；
在△AOE与△COF中，
，
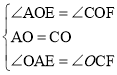∴△AOE≌△COF（ASA），
∴AE＝CF，
∴四边形AECF为平行四边形，
∵AE＝CE，
∴四边形AECF是菱形，
∵CE2＝BE2+BC2，
∴CE2＝（8﹣CE）2+16，
∴CE＝5cm，
∵AB＝8cm，BC＝4cm，
∴AC＝
＝
＝4
，
∵S菱形AECF＝5×4＝
×4×EF，
∴EF＝2cm，
故选：D．
练习册系列答案
相关题目
【题目】某学校组织健康知识竞赛，每班参加竞赛的人数相同，成绩为
，
，
，
四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
一班竞赛成绩统计图
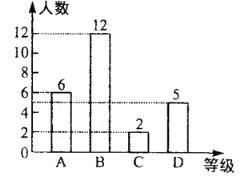
二班竞赛成绩统计图
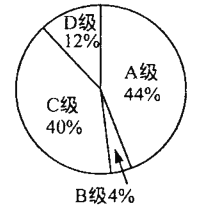
一班和二班竞赛成绩统计表（部分空缺）
成绩 班级 | 众数 | 中位数 | 优秀率 | 平均分 |
一班 | 90 |
|
| 87.6 |
二班 |
| 80 |
|
|
请根据以上图表的信息解答下列问题：
（1）求
，
，
的值.
（2）若全校共有750名学生参加竞赛，估计成绩优秀的学生有多少人？
