题目内容
已知：直线
过抛物线
的顶点P，如图所示．
（1）顶点P的坐标是 ；
（2）若直线y=ax+b经过另一点A（0，11），求出该直线的表达式；
（3）在（2）的条件下，若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称，求直线y=mx+n与抛物线的交点坐标．
解：（1）∵y=﹣x2﹣2x+3=﹣（x 2+2x）+3=﹣（x+1） 2+4，
∴P点坐标为：（﹣1，4）。
（2）将点P（﹣1，4），A（0，11）代入y=ax+b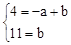得：
，解得：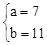
。
∴该直线的表达式为：y=7x+11。
（3）∵直线y=mx+n与直线y=7x+11关于x轴成轴对称，
∴y=mx+n过点P′（﹣1，﹣4），A′（0，﹣11）。
∴
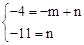，解得：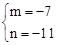
。
∴y=﹣7x﹣11。∴﹣7x﹣11=﹣x 2﹣2x+3。
解得：x1=7，x2=﹣2，此时y1=﹣60，y2=3。
∴直线y=mx+n与抛物线y=﹣x2﹣2x+3的交点坐标为：（7，﹣60），（﹣2，3）。
解析试题分析：（1）利用配方法求出图象的顶点坐标即可：
（2）利用待定系数法求一次函数解析式即可。
（3）根据关于x轴对称点的坐标性质，首先求出直线y=mx+n的解析式，进而得出直线y=mx+n与抛物线y=﹣x2﹣2x+3的交点坐标。
练习册系列答案
相关题目
经过点A（0，3），B（3，0），C（4，3）．
，同理
，所以AB的中点坐标为
．由勾股定理得
，所以A、B两点间的距离公式为
．
与x轴交于点A，与y轴交于点B，将△AOB绕点O顺时针旋转90°后得到△COD．
与x轴交于点A和点B，与y轴交于点C，已知点B的坐标为（3，0）．