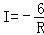题目内容
如图,抛物线 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
(1)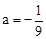 。抛物线的顶点坐标为(﹣
。抛物线的顶点坐标为(﹣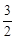 ,
,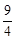 )。
)。
(2)M点的坐标是(﹣9,﹣4)。
(3)在抛物线对称轴上存在一点N,能够使d=|AN﹣CN|的值最大。理由见解析。
解析分析:(1)先把点B的坐标代入 ,可求得a的值,再利用配方法将一般式化为顶点式,即可求得抛物线的顶点坐标。
,可求得a的值,再利用配方法将一般式化为顶点式,即可求得抛物线的顶点坐标。
(2)先由抛物线的解析式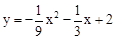 ,求出与x轴的交点A的坐标,与y轴的交点C的坐标,再由△AMC与△ABC的面积相等,得出这两个三角形AC边上的高相等,又由点B与点M都在AC的下方,得出BM∥AC,则点M既在过B点与AC平行的直线上,又在抛物线
,求出与x轴的交点A的坐标,与y轴的交点C的坐标,再由△AMC与△ABC的面积相等,得出这两个三角形AC边上的高相等,又由点B与点M都在AC的下方,得出BM∥AC,则点M既在过B点与AC平行的直线上,又在抛物线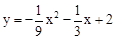 上,所以先运用待定系数法求出直线AC的解析式为y=
上,所以先运用待定系数法求出直线AC的解析式为y= x+2,再设直线BM的解析式为y=
x+2,再设直线BM的解析式为y= x+n,将点B(3,0)代入,求出n的值,得到直线BM的解析式为
x+n,将点B(3,0)代入,求出n的值,得到直线BM的解析式为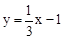 ,然后解方程组
,然后解方程组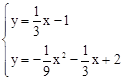 ,即可求出点M的坐标。
,即可求出点M的坐标。
(3)连接BC并延长,交抛物线的对称轴x=﹣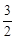 于点N,连接AN,根据轴对称的性质得出AN=BN,并且根据三角形三边关系定理得出此时d=|AN﹣CN|=|BN﹣CN|=BC最大.运用待定系数法求出直线BC的解析式,再将x=﹣
于点N,连接AN,根据轴对称的性质得出AN=BN,并且根据三角形三边关系定理得出此时d=|AN﹣CN|=|BN﹣CN|=BC最大.运用待定系数法求出直线BC的解析式,再将x=﹣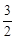 代入,求出y的值,得到点N的坐标,然后利用勾股定理求出d的最大值BC即可。
代入,求出y的值,得到点N的坐标,然后利用勾股定理求出d的最大值BC即可。
解:(1)∵抛物线 经过点B(3,0),
经过点B(3,0),
∴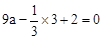 ,解得
,解得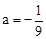 。
。
∴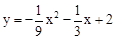 。
。
∵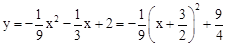 ,
,
∴抛物线的顶点坐标为(﹣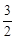 ,
,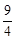 )。
)。
(2)∵抛物线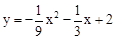 的对称轴为直线x=﹣
的对称轴为直线x=﹣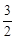 ,与x轴交于点A和点B,点B的坐标为(3,0),
,与x轴交于点A和点B,点B的坐标为(3,0),
∴点A的坐标为(﹣6,0)。
又∵当x=0时,y=2,∴C点坐标为(0,2)。
设直线AC的解析式为y=kx+b,
则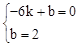 ,解得:
,解得: 。
。
∴直线AC的解析式为y= x+2。
x+2。
∵S△AMC=S△ABC,∴点B与点M到AC的距离相等。
又∵点B与点M都在AC的下方,∴BM∥AC。
设直线BM的解析式为y= x+n,将点B(3,0)代入,得
x+n,将点B(3,0)代入,得 ×3+n=0,解得n=﹣1。
×3+n=0,解得n=﹣1。
∴直线BM的解析式为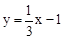 .
.
由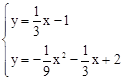 ,解得
,解得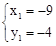 ,
, 。
。
∴M点的坐标是(﹣9,﹣4)。
(3)在抛物线对称轴上存在一点N,能够使d=|AN﹣CN|的值最大。理由如下:
∵抛物线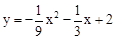 与x轴交于点A和点B,
与x轴交于点A和点B,
∴点A和点B关于抛物线的对称轴对称。
连接BC并延长,交直线x=﹣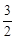 于点N,连接AN,则AN=BN,此时d=|AN﹣CN|=|BN﹣CN|=BC最大。
于点N,连接AN,则AN=BN,此时d=|AN﹣CN|=|BN﹣CN|=BC最大。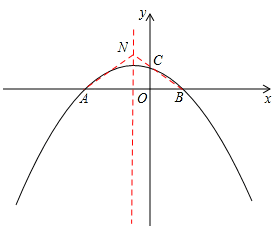
设直线BC的解析式为y=mx+t,将B(3,0),C(0,2)两点的坐标代入,
得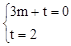 ,解得:
,解得: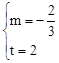 。
。
∴直线BC的解析式为y=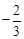 x+2。,
x+2。,
当x=﹣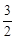 时,y=-
时,y=-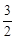 ×(﹣
×(﹣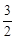 )+2=3。
)+2=3。
∴点N的坐标为(﹣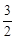 ,3),d的最大值为
,3),d的最大值为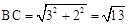 。
。

已知点(-1,y1)、(2,y2)、(3,y3)在反比例函数 的图象上.下列结论中正确的是
的图象上.下列结论中正确的是
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y1>y2 | D.y2>y3>y1 |
 过抛物线
过抛物线 的顶点P,如图所示.
的顶点P,如图所示.
 ,抛物线
,抛物线 (a≠0)经过点A(4,0)与点(﹣2,6).
(a≠0)经过点A(4,0)与点(﹣2,6).
 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数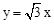 的图象的对称点为C。
的图象的对称点为C。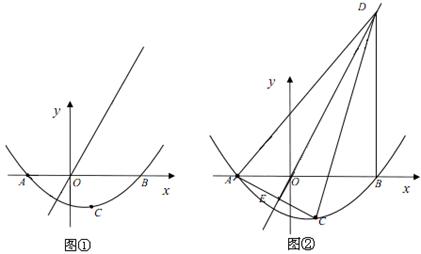
 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为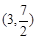 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。
 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。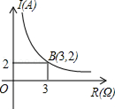
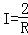 B.
B.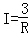 C.
C.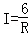 D.
D.